CHO HÀM SỐ f(x) THOẲ MÃN f(ab)=f(a)+f(b)và f(1)=2016 tính f(2014)
b)CM hàm số trên là hàm hằng
Những câu hỏi liên quan
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số y = f(x) xác định với mọi x thuộc z (x >0) và thỏa mãn f(1)=1, f(a+b)= f(a) +f(b) - 2f(ab).
Tính f(2014) và f(2015)
Cho hàm số f(x) có đạo hàm trên R và thỏa mãn f(2016) a, f(2017) b,
a
;
b
∈
ℝ
. Giá trị
I
∫
2017
2016
2015
f
x
.
f
2014
x
d
x
bằng: A.
I
b
2017...
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R và thỏa mãn f(2016) = a, f(2017) = b, a ; b ∈ ℝ . Giá trị I = ∫ 2017 2016 2015 f ' x . f 2014 x d x bằng:
A. I = b 2017 - a 2017
B. I = a 2016 - b 2016
C. I = a 2015 - b 2015
D. I = b 2015 - a 2015
Chọn C.
Đặt t = f ( x ) → d t = f ' x d x . Đổi cận: x = 2016 → t = f ( 2016 ) = a x = 2017 → t = f ( 2017 ) = b
Khi đó
Đúng 0
Bình luận (0)
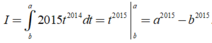
Cho hàm số f(x) xác định với mọi x thỏa mãn f (a+b) = f (a.b) và f (-1/2) = -1/2 . Tính f ( 2016)
Với mọi x thỏa mãn: f( a + b ) = f (ab)
=>f( 0 ) = f( -1/2 . 0 ) = f ( -1/2 + 0 ) = f( -1/2 ) = -1/2
=> f ( 2006 ) = f ( 2006 + 0 ) = f(2006 . 0 ) = f(0 ) = -1/2
Cho hàm số f(x) xác định với mọi x thuộc R thỏa mãn f(a+b) = f (a.b) với mọi a, b thuộc R và f(-1/2)=-1/2. Tính f(2016)
Cho hàm số y f(x) thỏa mãn f(x)
(
x
+
1
)
e
x
và
∫
f
(
x
)
d
x
(
a
x
+
b
)
e
x
+
c
, với a, b, c là các hằng số. Khi đó A. a + b 0 B. a + b 3 C. a + b 2 D. a + b 1
Đọc tiếp
Cho hàm số y = f(x) thỏa mãn f'(x) = ( x + 1 ) e x và ∫ f ( x ) d x = ( a x + b ) e x + c , với a, b, c là các hằng số. Khi đó
A. a + b = 0
B. a + b = 3
C. a + b = 2
D. a + b = 1
Cho hàm số yf(x) thỏa mãn
f
(
x
)
(
x
+
1
)
e
x
và
∫
f
(
x
)
d
x
(
a
x
+
b
)
e
x
+
c
với a, b, c là các hằng số. Khi đó: A. a + b 0 B. a + b 3 C. a + b 2 D. a + b 1
Đọc tiếp
Cho hàm số y=f(x) thỏa mãn f ' ( x ) = ( x + 1 ) e x và ∫ f ( x ) d x = ( a x + b ) e x + c với a, b, c là các hằng số. Khi đó:
A. a + b = 0
B. a + b = 3
C. a + b = 2
D. a + b = 1
Cho F(x) là một nguyên hàm của hàm số f(x)|1+x|-|1-x| trên tập R và thỏa mãn F(1) 3.Tính tổng F(0)+F(2)+F(-3).
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f(x)=|1+x|-|1-x| trên tập R và thỏa mãn F(1)= 3.Tính tổng F(0)+F(2)+F(-3).
