mng giúp mik zới ạ. Mik cảm ơn nhìu ạ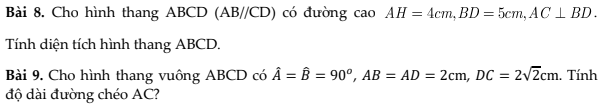

Những câu hỏi liên quan
giúp mik với ạ, mik đang cần gấp! cảm ơn mng nhìu!
Đọc tiếp
giúp mik với ạ, mik đang cần gấp! cảm ơn mng nhìu!
\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Em hãy thuyết minh về đại hội thể dục thể thao ở địa phương em.
Mng giúp mik vs ạ, mik đag cần rất gấp.
Cảm ơn mng nhìu <3
Tính nhanh
23 x 58 - 30 x 23 + 28 x 77 =
giúp mik zới mn ui , mik cần gấp lắm , làm ơn giúp mình ik mà mn , năn nỉ mn đó , giải tích cả cahs làm cho mik nhé , thank you mn nhìu ạ , kết quả gợi ý là 2800 mik mong các bạn sẽ trả lời đúng kết quả mà mik gợi ý , mong mn sẽ giúp mik , cảm ơn mn nhìu ạ
=23 x (58-30) + 28 x 77
=23 x 28 +28 x 77
=28 x (23+77)
=28 x 100
=2800
học tốt bạn nhé
bài này là dạng nâng cao về toán tính nhanh, mik nghĩ là ẽ ít bạn trả lời đc
Xem thêm câu trả lời
giúp mik với mik đang cần gấp đó mn cảm ơn mn nhìu ạ=((



TỪ CÂU 1 ĐẾN 20 NHA Ạ CẢM ƠN NHÌU MIK ĐANG CẦN GẤP-((
1.A
2.A
3.B
4.C
5.B
6.C
7.A
8.A
9.B
10.A
11.B
12.A
13.C
14.B
15.B
16.A
17.A
18.A
19.A
20.C
Đúng 0
Bình luận (0)
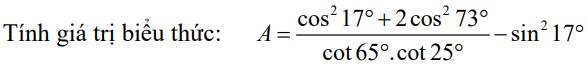
Mng giúp mik với ạ. Mik cảm ơn.
\(A=\dfrac{\cos^217^o+2\cos^273^o}{\cot65^o\cot25^o}-\sin^217^o\)
\(A=\dfrac{\left(\cos^217^o+\cos^273^o\right)+\cos^273^o}{\tan25^o\cot25^o}-\sin^217^o\)
(áp dụng công thức \(\cot\alpha=\tan\left(90^o-\alpha\right)\))
\(A=\left(\cos^217^o+\sin^217^o\right)+\sin^217^o-\sin^217^o\)
(áp dụng công thức \(\tan\alpha.\cot\alpha=1\) và \(\cos\alpha=\sin\left(90^o-\alpha\right)\))
\(A=1\)
Đúng 3
Bình luận (0)
mng giải hẳn ra giúp mik ạ. mik cảm ơn
Đọc tiếp
mng giải hẳn ra giúp mik ạ. mik cảm ơn
Lời giải:
Theo đề ta có:
\(\text{sđc(AD)}=\frac{1}{3}\text{sđc(AB)}=\frac{1}{9}[\text{sđc(AB)+sđc(BC)+sđc(CD)}]\)
\(=\frac{1}{9}(360^0-\text{sđc(AD)})\)
\(\Rightarrow \text{sđc(AD)}=36^0\)
\(\widehat{BEC}=\frac{\text{sđc(BC)-sđc(AD)}}{2}=\frac{3\text{sđc(AD)}-\text{sđc(AD)}}{2}=\text{sđc(AD)}=36^0\)
Đúng 1
Bình luận (0)
mng giúp e câu này zới e cám ơn mng gấc nhìu ạ <333
giải hệ phương trình sau :
2x-5y=11
3x+4y=5
\(\Leftrightarrow\left\{{}\begin{matrix}8x-20y=44\\15x+20y=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
GIÚP MIK BÀI 1 TỰ LUẬN VỚI Ạ MIK CẢM ƠN NHÌU Ạ
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(BH^2=HA\cdot HC\)
\(\Leftrightarrow BH^2=2\cdot6=12\)
hay \(BH=2\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBHA vuông tại H, ta được:
\(BA^2=BH^2+HA^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{3}\right)^2+2^2=12+4=16\)
hay BA=4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow BC^2=8^2-4^2=48\)
hay \(BC=4\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{CA}=\dfrac{4\sqrt{3}}{8}=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{A}=\dfrac{BA}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
c) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{\sqrt{3}}{2}\)
nên \(\widehat{A}=60^0\)
\(\Leftrightarrow\widehat{C}=30^0\)
Đúng 0
Bình luận (0)

giúp mik vs ạ mik cảm ơn nhìu
Tìm lỗi sai trong câu:
What you do?
giúp mik zới ạ
mik cảm ơn<3



























