Giúp mình với ạaaaaa TvT
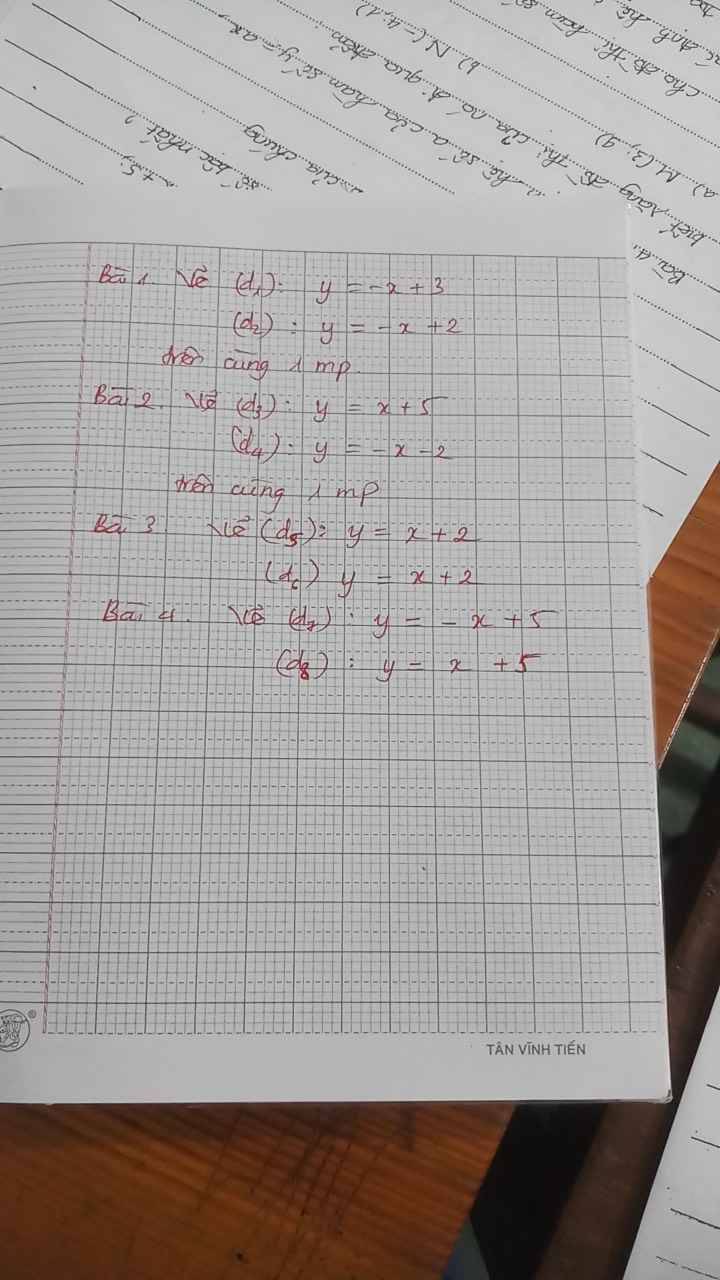
giúp mình với ạaaaaa
 giúp mình câu 2 với ạaaaaa
giúp mình câu 2 với ạaaaaa
Câu 2:
=>x=1-y và m(1-y)-y=2m
=>x=1-y và m-my-y=2m
=>x=1-y và y(-m-1)=m
=>x=1-y và y=-m/m+1
=>x=1+m/m+1=(m+2)/m+1 và y=-m/m+1
Để x,y nguyên thì m+1+1 chia hết cho m+1 và -m-1+1 chia hết cho m+1
=>\(m+1\in\left\{1;-1\right\}\)
mà m<>0
nên m=-2
Giúp mình bìa 7 ,8 với ạaaaaa 
giúp mình với TvT
\(a,\) Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\\ \dfrac{a^2-b^2}{c^2-d^2}=\dfrac{b^2k^2-b^2}{d^2k^2-d^2}=\dfrac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\dfrac{b^2}{d^2}\\ \Rightarrow\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\left(\dfrac{a-b}{c-d}\right)^4=\left(\dfrac{bk-b}{dk-d}\right)^4=\left(\dfrac{b\left(k-1\right)}{d\left(k-1\right)}\right)^4=\dfrac{b^4}{d^4}\\ \dfrac{a^4+b^4}{c^4+d^4}=\dfrac{b^4k^4+b^4}{d^4k^4+d^4}=\dfrac{b^4\left(k^4+1\right)}{d^4\left(k^4+1\right)}=\dfrac{b^4}{d^4}\\ \RightarrowĐpcm\)
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\\ \dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}=\dfrac{\left(bk+b\right)^2}{\left(dk+d\right)^2}=\dfrac{\left[b\left(k+1\right)\right]^2}{\left[d\left(k+1\right)\right]^2}=\dfrac{b^2\left(k+1\right)^2}{d^2\left(k+1\right)^2}=\dfrac{b^2}{d^2}\\ \RightarrowĐpcm\)
Giúp mình với mn TvT
a: Xét ΔDHE vuông tại H và ΔDKF vuông tại K có
DE=DF
\(\widehat{D}\) chung
Do đó: ΔDHE=ΔDKF
Suy ra: DH=DK
hay ΔDKH cân tại D
Giúp mình với ạ.Chiều nay mình nộp rồi TvT

Giúp mình với ạ, mai mình kiểm tra rồi TvT
uses crt;
var s:real;
a,i,n:integer;
begin
clrscr;
readln(a,n);
s:=1;
for i:=1 to n do
if i mod 2=0 then s:=s*(a+i);
writeln(s:0:0);
readln;
end.
GIÚP EM VỚI ẠAAAAA


giúp emmmm với ạaaaaa
45. I know how to use this machine, I can help you.
46. excited about the journey.
47. Peter is the best student in my class who can solve this difficult problem.
48. very good at typing.
GIÚP EM VỚI ẠAAAAA
Ta có: \(x^2-3x+2=\left(1-x\right)\sqrt{3x-2}\) \(\left(x\ge\dfrac{2}{3}\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-\left(1-x\right)\sqrt{3x-2}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2+\sqrt{3x-2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(TM\right)\\\sqrt{3x-2}=2-x\left(1\right)\end{matrix}\right.\)
Xét (1) ta có: \(\left\{{}\begin{matrix}2-x\ge0\\3x-2=4-4x+x^2\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}2\ge x\\x^2-7x+6=0\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x\le2\\\left[{}\begin{matrix}x=6\left(KTM\right)\\x=1\left(TM\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy nghiệm của phương trình là x=1
ĐKXĐ : x \(\ge\dfrac{2}{3}\)
Ta có \(\left(x-1\right)\left(x-2\right)=\sqrt{3x-2}\left(1-x\right)\)
<=> \(\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\sqrt{3x-2}=2-x\end{matrix}\right.\)
Khi x - 1 = 0 <=> x = 1 (tm)
Khi \(\sqrt{3x-2}=2-x\)
<=> \(\left\{{}\begin{matrix}3x-2=x^2-4x+4\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-7x+6=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-6\right)=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow x=1\)
Vậy phương trình 1 nghiêm \(x=1\)
\(ĐK:x\ge\dfrac{2}{3}\)
\(\Leftrightarrow\left(x-2\right)^2+x-2=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow\left(x-2\right)\left(x-2+1\right)=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=\left(1-x\right)\sqrt{3x-2}\)
\(\Leftrightarrow x-2=-\sqrt{3x-2}\)
\(\Leftrightarrow2-x=\sqrt{3x-2}\)
\(\Leftrightarrow\left(2-x\right)^2=\left(\sqrt{3x-2}\right)^2\)
\(\Leftrightarrow4-4x+x^2=3x-2\)
\(\Leftrightarrow x^2-7x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\) (vi-et )
Vậy S=\(\left(1;6\right)\)