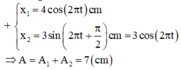Cho phương trình x=4cos(2πt-π/3) Tìm t để x=0

Những câu hỏi liên quan
Một vật dao động điều hòa có phương trình x = 4cos(2πt + π/3)(cm). Pha dao động là
A. 2π.
B. 4.
C.π/3.
D.(2πt + π/3)
Đáp án D
Phương pháp: Sử dụng lí thuyết về dao động điều hoà
Pha dao động: (2πt + π/3)
Đúng 0
Bình luận (0)
Một vật dao động điều hòa với phương trình x = 4cos(2πt + π/2)cm. Vận tốc cực đại của vật trong quá trình dao động bằng
A. 2πcm/s.
B. - 8πcm/s.
C. 8πcm/s.
D. 4πcm/s.
Đáp án C
Phương pháp: Áp dụng công thức tính vận tốc cực đại của vật dao động điều hoà v max = Aω
Vận tốc cực đại mà vật đạt được trong quá trình dao động là v max = Aω = 2 π . 4 = 8 π
Đúng 0
Bình luận (0)
Con lắc đơn có dây treo dài 1 m, đang dao động điều hòa với phương trình s = 4cos(2πt + π/3) cm. Tại thời điểm ban đầu, t = 0, ly độ góc của con lắc bằng
A. 0,02 rad
B. 0,015 rad
C. 0,005 rad
D. 0,01 rad
Chọn đáp án A
s = l α → α = 0,04cos(2πt + π/3) rad → t = 0 thì α = 0,04cos(π/3) = 0,02 rad
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
Một chất điểm dao động điều hòa theo phương trình
x
4
cos
(
2
πt
/
3
)
(x tính bằng cm; t tính bằng s). Kể từ t 0, chất điểm đi qua vị trí có li độ x -2 cm lần thứ 2017 tại thời điểm A. 3015 s. B. 6030 s. C. 3016 s. D. 3025 s.
Đọc tiếp
Một chất điểm dao động điều hòa theo phương trình x = 4 cos ( 2 πt / 3 ) (x tính bằng cm; t tính bằng s). Kể từ t = 0, chất điểm đi qua vị trí có li độ x = -2 cm lần thứ 2017 tại thời điểm
A. 3015 s.
B. 6030 s.
C. 3016 s.
D. 3025 s.
Chọn D.
Cách 1: Giải PTLG. T = 2 π ω = 3
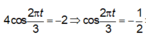
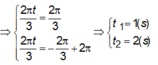
2017 2 = 1008 d ư 1
![]()
Cách 2: Dùng VTLG
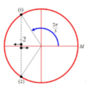
Quay một vòng qua li độ x = -2 cm là hai lần. Để có lần thứ
2017 = 2.1008 + 1 thì phải quay 1008 vòng và quay thêm một góc 2 π / 3 tức tổng góc quay: ∆ φ = 1008 . 2 π + 2 π / 3
thời gian:
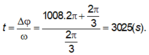
Đúng 0
Bình luận (0)
Một vật tham gia đồng thời hai dao động điều hòa cùng phương có phương trình lần lượt là
x
1
4
cos
(
2
π
t
)
c
m
và
x
2
3
sin
(
2
π
t
+
π
/
2
)
c...
Đọc tiếp
Một vật tham gia đồng thời hai dao động điều hòa cùng phương có phương trình lần lượt là x 1 = 4 cos ( 2 π t ) c m và x 2 = 3 sin ( 2 π t + π / 2 ) c m . Biên độ dao động tổng hợp bằng
A. 7 cm.
B. 1 cm.
C. 4 cm.
D. 5 cm.
Chọn đáp án A
x 1 = 4 cos 2 π t c m x 2 = 3 sin 2 π t + π 2 c m = 3 cos 2 π t ⇒ A = A 1 + A 2 = 7 c m
Đúng 0
Bình luận (0)
Một vật tham gia đồng thời hai dao động điều hòa cùng phương có phương trình lần lượt là
x
1
4
cos
(
2
π
t
)
c
m
v
à
x
2
3
sin
(
2
π
t
+
π...
Đọc tiếp
Một vật tham gia đồng thời hai dao động điều hòa cùng phương có phương trình lần lượt là x 1 = 4 cos ( 2 π t ) c m v à x 2 = 3 sin ( 2 π t + π / 2 ) c m . Biên độ dao động tổng hợp bằng
A. 7 cm.
B. 1 cm.
C. 4 cm.
D. 5 cm.
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5cos(2πt – π/3) (x tính bằng cm; t tính bằng s). Kể từ t = 0, lò xo không biến dạng lần đầu tại thời điểm
A. 5/12 s
B. 1/6 s
C. 2/3 s
D. 11/12 s
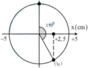
Lò xo không biến dạng tại vị trí cân bằng.
→ Biểu diễn dao động của vật tương ứng trên đường tròn.
Từ hình vẽ ta thấy rằng khoảng thời gian tương ứng là t = 5T/12 = 5/12
Đáp án A
Đúng 0
Bình luận (0)
Một con lắc lò xo nằm ngang dao động theo phương trình x=5cos(2πt-π/3)(cm) ( x tính bằng cm; t tính bằng s). Kể từ t=0, lực đàn hồi đổi chiều lần đầu tại thời điểm
A. 2/3 s.
B. 11/12 s.
C. 1/6 s.
D. 5/12s
Đáp án D
Phương pháp: Sử dụng lí thuyết về lực đàn hồi trong dao động điều hòa của CLLX ngang và đường tròn lượng giác
Cách giải:
+ Đối với CLLX ngang thì lực đàn hồi đổi chiều tại VTCB
+ Biểu diễn trên đường tròn lượng giác :
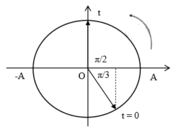
Góc quét được:
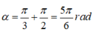
=> Từ t = 0 thì vật đi qua VTCB lần đầu tại thời điểm:
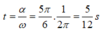
Đúng 0
Bình luận (0)
Một vật dao động điều hòa với phương trình x= 4cos(2πt - π/3)cm. Quãng đường nhỏ nhất vật đi được trong khoảng thời gian 2/3 chu kỳ dao động là ( lấy gần đúng):
A. 12cm
B.10,92cm
C.9,07cm
D.10,26cm
\(\dfrac{2}{3}T=\dfrac{T}{2}+\dfrac{T}{6}\)
+ Trong thời gian T/2 quãng đường vật đi được luôn là 2A (không có min, max)
+ Như vậy, ta cần tìm quãng đường nhỏ nhất trong thời gian T/6.
Biểu diễn dao động bằng véc tơ quay, trong thời gian T/6 thì véc tơ quay được góc là: 360/6 = 600.
Quãng đường nhỏ nhất khi vật đi tốc độ bé nhất --> Vật đi quanh vị trí biên.
\(\Rightarrow S_{min}=2.(A-A\cos 30^0)=2A(1-\cos 30^0)\)
Tổng quãng đường nhỏ nhất là: \(2A+2A(1-\cos 30^0)=2A(2-\cos 30^0)==2.4.(2-\cos 30^0)=9,07cm\)
Chọn đáp án C.
Đúng 1
Bình luận (1)