Viết phương trình đường thẳng (d') song song với (d) và tiếp xúc với (P)

Những câu hỏi liên quan
Tronh hệ trực Oxy cho điểm I(1,3) và đường thẳng d: 3x+4y+5=0 a) viết PTTQ đường thẳng qua I và song song với d b) viết phương trình đường tròn tâm I và tiếp xúc với d
`a)` Gọi đường thẳng `\Delta` song song với `d` là: `3x+4y+c=0` `(c ne 5)`
Mà `I in \Delta`
`=>2.1+4.3+c=0<=>c=-14` (t/m)
`=>PTTQ` của `\Delta` là: `3x+4y-14=0`
`b)` Có: `R=d(I;d)=[|3.1+4.3+5|]/[\sqrt{3^2+4^2}]=4`
`=>` Ptr đường tròn tâm `I` bán kinh `R=4` là:
`(x-1)^2+(y-3)^2=16`
Đúng 0
Bình luận (1)
Bài 14: Cho (P): \(y=x^2\)
1. Gọi A và B là hai điểm thuộc (P) có hoành độ lần lượt là -1 và 2. Viết phương trình đường thẳng AB
2. Viết Phương trình đường thẳng (d) song song với AB và tiếp xúc với (P)
1.
\(x=-1\Rightarrow y=1\Rightarrow A\left(-1;1\right)\)
\(x=2\Rightarrow y=4\Rightarrow B\left(2;4\right)\)
Phương trình đường thẳng AB có dạng \(y=ax+b\) đi qua A và B nên ta có hệ:
\(\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\Rightarrow y=x+2\left(AB\right)\)
2.
\(\left(d\right)//\left(AB\right)\Rightarrow x-y+c=0\left(d\right)\)
Phương trình hoành độ giao điểm của \(\left(d\right);\left(P\right)\):
\(x+c=x^2\)
\(\Leftrightarrow x^2-x-c=0\)
\(\Delta=1+4c=0\Leftrightarrow c=-\dfrac{1}{4}\)
\(\Rightarrow x-y-\dfrac{1}{4}=0\left(d\right)\)
Đúng 2
Bình luận (0)
Bài 9: Cho hàm số (P): y = \(x^2\)
1. Vẽ (P)
2. Gọi A,B là hai điểm thuộc (P) có hoành độ lần lượt là -1 và 2. Viết phương trình đường thẳng AB
3. Viết Phương trình đường thẳng (d) song song với AB và tiếp xúc với (P)
Cho đường tròn (C): x 2 + y 2 + 2x + 4y = 0 và đường thẳng d: 2x + y - 3 = 0. Phương trình đường thẳng d’ song song với d và tiếp xúc với đường tròn (C) là:
A. 2x + y - 1 = 0
B. 2x + y + 9 = 0
C. Cả A và B đều đúng
D. Không tồn tại đường thẳng d’
Đáp án: C
Ta có:
(C): x 2 + y 2 + 2x + 4y = 0 ⇔ (x + 1 ) 2 + (y + 2 ) 2 = 5
⇒ I(-1;-2), R = 5
Vì d’ song song với d nên d': 2x + y + c = 0, (c ≠ -3)
Đường thẳng d’ tiếp xúc với (C) nên
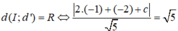
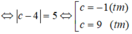
Vậy phương trình đường thẳng d’ là: 2x + y - 1 = 0 hoặc 2x + y + 9 = 0
Đúng 0
Bình luận (0)
Cho y=\(-x^2\)(P) ; y=2x (D)
Viết phương trình đường thẳng (D1) song song với (D) và tiếp xúc (P)
Trong mp tọa độ Oxy, cho đường tròn (C): x2+y2-2x+8y+1=0 và đường thẳng d: 5x+12y-6=0. Phương trình các đường thẳng song song với d và tiếp xúc với (C) là
Đường tròn (C) tâm \(I\left(1;-4\right)\) bán kính \(R=4\)
Tiếp tuyến d' song song d nên có dạng: \(5x+12y+c=0\) (với \(c\ne-6\))
d' tiếp xúc (C) khi và chỉ khi:
\(d\left(I;d'\right)=R\Leftrightarrow\dfrac{\left|5.1-12.4+c\right|}{\sqrt{5^2+12^2}}=4\)
\(\Leftrightarrow\left|c-43\right|=52\Rightarrow\left[{}\begin{matrix}c=95\\c=-9\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}5x+12y+95=0\\5x+12y-9=0\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Trong cùng hệ trục tọa độ Oxy cho parabol (P) : \(y=-\frac{x^2}{4}\) và đường thẳng (D) : \(y=\frac{x}{2}-2\) . Viết phương trình đường thẳng (d) song song với (D) và tiếp xúc với (P)
No chưa học lớp 9 đừng mong làm
Gọi phương trình đường thẳng (d) là \(y=ax+b\) \(\left(a\ne0\right)\)
Để \(\left(d\right)//\left(D\right)\)\(\Leftrightarrow\hept{\begin{cases}a=\frac{1}{2}\\b\ne-2\end{cases}}\)
Phương trình hoành đệ giao điểm (P) và (d)
\(\frac{-x^2}{4}=ax+b\)
Thay \(a=\frac{1}{2}\)vào, ta có:
\(\frac{-x^2}{4}=\frac{1}{2}x+b\)
\(\Leftrightarrow\frac{x^2}{4}+\frac{1}{2}x+b=0\)
\(\Leftrightarrow x^2+2x+4b=0\)(1)
Ta có \(\Delta'=1^2-1.4b\)
\(=1-4b\)
Để (d) tiếp xúc (P) \(\Leftrightarrow\) Phương trình (1) có nghiệm kép
\(\Leftrightarrow\Delta'=0\)
\(\Leftrightarrow1-4b=0\)
\(\Leftrightarrow4b=1\)
\(\Leftrightarrow b=\frac{1}{4}\left(TM\right)\)
Vậy phương trình đường thẳng (d): \(y=\frac{1}{2}x+\frac{1}{4}\)
Viết phường trình đường thẳng (D1) song song (D) y=2x và tiếp xúc với (P)=y=\(-x^2\)
vì D1 song song vs D
=> D1 = 2x + b
xét pt hoành độ giao điểm ta có
-x^2 = 2x +b <=> x^2 + 2x + b = 0
xét đen ta của phương trình trên ta đc: 4-4b
mà D1 tiếp xúc vs P Nên 4 - 4b = 0 => b=1
vậy đg thẳng D1 có dạng y= 2x+1
Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S):(S):
x
2
+
y
2
+
z
2
– 10x + 2y +26z + 170 0và song song với hai đường thẳng:
d
:
x
-
5
+
2
t...
Đọc tiếp
Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S):
(S): x 2 + y 2 + z 2 – 10x + 2y +26z + 170 = 0
và song song với hai đường thẳng: d : x = - 5 + 2 t y = 1 - 3 t z = - 13 + 2 t v à d ' : x = - 7 + 3 t ' y = - 1 - 2 t z = 8
+ Mặt cầu
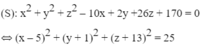
Vậy (S) có tâm I(5; -1; -13), bán kính R = 5.
+ (α) song song với d và d’
⇒ (α) nhận vtcp của d và d’ là 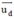 = (2; -3; 2) và
= (2; -3; 2) và 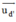 = (3 ; -2 ; 0) là các vtcp
= (3 ; -2 ; 0) là các vtcp
⇒ (α) nhận 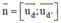 = (4; 6; 5) là vtpt
= (4; 6; 5) là vtpt
⇒ (α): 4x + 6y + 5z + D = 0.
(α) tiếp xúc với (S)
⇒ d(I; α) = R
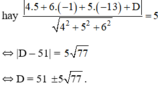
Vậy có hai mặt phẳng thỏa mãn là:
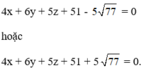
Đúng 0
Bình luận (0)
Cho y=\(-x^2\)(P), y=2x(D)
Viết phương trinhf đường thẳng (d1) song song với (D) và tiếp xúc với (P)
Mình học lớp 7 oke ko bít


















