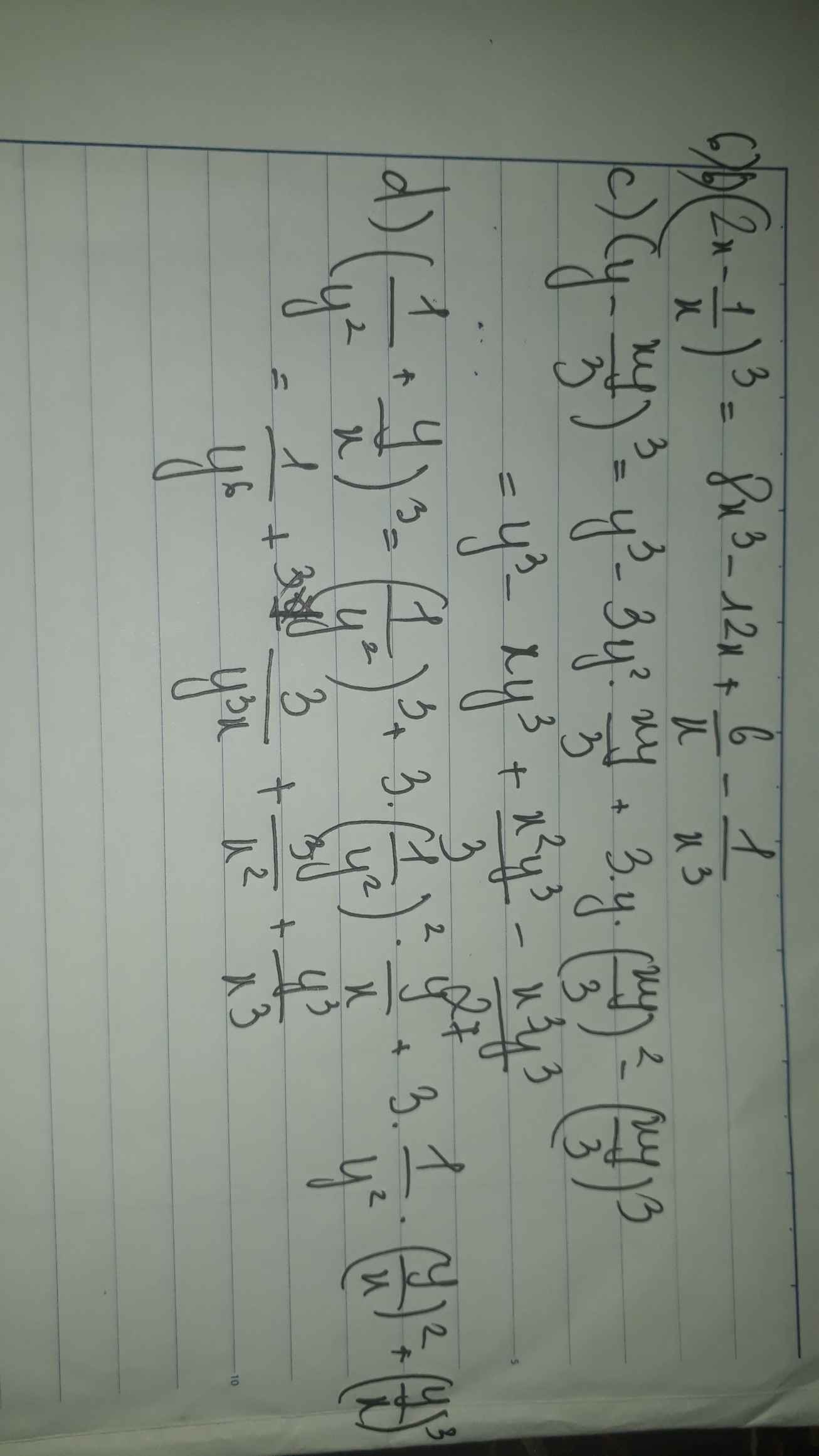Giúp em với ạ, mai em phải nộp rồi

Những câu hỏi liên quan
giúp em với ạ mai em phải nộp bài rồi ạ:D
Gọi tia đối của tia AB là AE
=>AD là phân giác của \(\widehat{EAC}\)
Xét ΔABC có \(\widehat{EAC}\) là góc ngoài tại đỉnh A
nên \(\widehat{EAC}=\widehat{ABC}+\widehat{ACB}=80^0\)
AD là phân giác của góc EAC
=>\(\widehat{EAD}=\widehat{CAD}=\dfrac{\widehat{EAC}}{2}=\dfrac{80^0}{2}=40^0\)
\(\widehat{DAC}=\widehat{ACB}\left(=40^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
Đúng 0
Bình luận (0)
giúp em 7 bài này với ạ:(
sáng mai phải nộp bài rồi ạ
Bài 6:
Xét ΔOAC vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)(hai góc đối đỉnh)
Do đó: ΔOAC=ΔOBD
=>OC=OD
Bài 7:
a: Ta có: \(\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}+90^0=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}=90^0\)
mà \(\widehat{DAB}+\widehat{DBA}=90^0\)
nên \(\widehat{DBA}=\widehat{CAE}\)
Xét ΔABD vuông tại A và D và ΔCAE vuông tại E có
AB=AC
\(\widehat{DBA}=\widehat{EAC}\)
Do đó: ΔABD=ΔCAE
b: ta có: ΔABD=ΔCAE
=>DB=AE và AD=CE
DB+CE=DA+AE=DE
Đúng 0
Bình luận (0)
Dạ giải giúp em với ạ mai em phải nộp rồi ạ
Nếu được thì giải hộ em câu b,c thôi cũng được ạ
a: góc OBA+góc OCA=90+90=180 độ
=>ABOC nội tiếp
b: góc OIE=góc OCE=90 độ
=>OICE là tứ giác nội tiếp
=>góc OEI=góc OCI
=>góc OEI=góc OCB
OBAC nội tiếp
=>góc OCB=góc OAB
=>góc OEI=góc OAB
=>góc OEI=góc OAI
=>OIAE nội tiếp
Đúng 0
Bình luận (0)

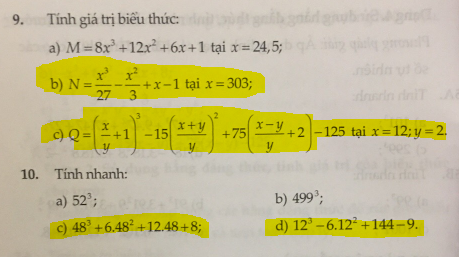 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
a) Ta có: \(\left(3x+1\right)^3\)
\(=\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2+1^3\)
\(=27x^3+27x^2+9x+1\)
b) Ta có: \(\left(2x-\dfrac{1}{x}\right)^3\)
\(=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot\dfrac{1}{x}+3\cdot2x\cdot\left(\dfrac{1}{x}\right)^2-\left(\dfrac{1}{x}\right)^3\)
\(=8x^3-12x+\dfrac{6}{x}-\dfrac{1}{x^3}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
MỌI NGƯỜI GIÚP EM GẤP Ạ MAI EM PHẢI NỘP RỒI !!!!!!!!

Mọi người ai làm giúp em câu 4 với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
Hãy tả lại cơn mưa xuân ở nơi em ở.(khoảng 2 trang rưỡi ạ)
MỌI NGƯỜI GIÚP EM VỚI Ạ,EM CẦN GẤP,MAI EM PHẢI NỘP CHO CÔ GIÁO RỒI Ạ!!!
Ai làm giúp em câu 3 và 4 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
Mọi người giúp em bài này vs ạ ! Em cần gấp lắm ạ , mai em phải nộp rồi ! Em cảm ơn !