vẽ hình minh họa cho câu sau tập hợp các điểm nằm trong goc xOy và cách đều hai cạnh của góc đó là tia phân giác của góc xOy

Những câu hỏi liên quan
Cho góc nhọn xOy và điểm M nằm trong góc đó. Chứng minh rằng nếu M cách đều hai cạnh của góc xOy thì M nằm trên tia phân giác của góc này.
Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng.
(1) Tập hợp các điểm cách A cố định một khoảng 3cm. (2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm.
(5) Là đường trung trực của đoạn thẳng AB. (6) là hai đường thẳng song song với a và cách a một khoảng 3cm. (7) là đường tròn t...
Đọc tiếp
Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng.
| (1) Tập hợp các điểm cách A cố định một khoảng 3cm. (2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm. |
(5) Là đường trung trực của đoạn thẳng AB. (6) là hai đường thẳng song song với a và cách a một khoảng 3cm. (7) là đường tròn tâm A bán kính 3cm. (8) là tia phân giác của góc xOy |
Ghép các ý:
(1) với (7)
(2) với (5)
(3) với (8)
(4) với (6)
Đúng 0
Bình luận (0)
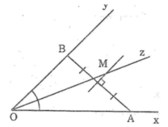
Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy. Hãy tìm điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy); cách đều Ox, Oy và cách đều A, B.
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
Đúng 0
Bình luận (0)
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề: Áp một lề của thước vào cạnh Ox, kẻ đường thẳng a theo lề kia. Làm tương tự với cạnh Oy, ta kẻ được đường thẳng b. Gọi M là giao điểm của a và b, ta có OM là tia phân giác của góc xOy. Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy. (Gợi ý: Dựa vào bài tập 12 chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai lề của chiếc thước) rồi áp dụng định lí 2) Hình 31
Đọc tiếp
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề:
Áp một lề của thước vào cạnh Ox, kẻ đường thẳng a theo lề kia.
Làm tương tự với cạnh Oy, ta kẻ được đường thẳng b.
Gọi M là giao điểm của a và b, ta có OM là tia phân giác của góc xOy.
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy.
(Gợi ý: Dựa vào bài tập 12 chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai lề của chiếc thước) rồi áp dụng định lí 2)
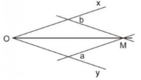
Hình 31
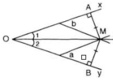
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Trong các mệnh đề sau a. Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó. b. Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó. c. Góc tạo bởi hai tia phân giác của hai góc kề bù là góc nhọn. d. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường dài nhất. Số mệnh đề đúng là: A. 1. B. 2 C. 3 D. 4
Đọc tiếp
Trong các mệnh đề sau
a. Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
b. Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
c. Góc tạo bởi hai tia phân giác của hai góc kề bù là góc nhọn.
d. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường dài nhất.
Số mệnh đề đúng là:
A. 1.
B. 2
C. 3
D. 4
Đáp án: B
a, b đúng.
c sai vì Góc tạo bởi hai tia phân giác của hai góc kề bù là góc vuông không phải góc nhọn.
d sai vì Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường ngắn nhất không phải dài nhất.
Đúng 0
Bình luận (0)
Vẽ hình theo cách diễn đạt sau ( Mỗi ý là 1 hình ) :1) Vẽ góc bẹt xOy.2) Vẽ góc xOy, điểm A nằm trong góc xOy, điểm B nằm ngoài góc xOy.3) Vẽ góc xOy, tia Oz nằm giữa hai tia Ox và Oy4) Vẽ góc nCm và nCt sao cho tia Cm nằm giữa hai tia Cn và Ct5) Vẽ các góc xOy; yOz; zOt và tOx sao cho góc xOz và yOt là các góc bẹt6) Vẽ các góc xOy; yOz; zOt sao cho ia Oz nằm trong góc xOy; tia Oy nằm trong góc zOt và xOt là góc bẹt7) Vẽ các góc xOy; yOz; zOt và tOx sao cho xOz là góc bẹt và hai tia Oy, Ot nằm t...
Đọc tiếp
Vẽ hình theo cách diễn đạt sau ( Mỗi ý là 1 hình ) :
1) Vẽ góc bẹt xOy.
2) Vẽ góc xOy, điểm A nằm trong góc xOy, điểm B nằm ngoài góc xOy.
3) Vẽ góc xOy, tia Oz nằm giữa hai tia Ox và Oy
4) Vẽ góc nCm và nCt sao cho tia Cm nằm giữa hai tia Cn và Ct
5) Vẽ các góc xOy; yOz; zOt và tOx sao cho góc xOz và yOt là các góc bẹt
6) Vẽ các góc xOy; yOz; zOt sao cho ia Oz nằm trong góc xOy; tia Oy nằm trong góc zOt và xOt là góc bẹt
7) Vẽ các góc xOy; yOz; zOt và tOx sao cho xOz là góc bẹt và hai tia Oy, Ot nằm trên hai nửa mặt phẳng đối nhau bờ xz
Câu 1: Cho góc xoy khác góc bẹt, tia oz nằm trong góc đó , chúng tỏ rằnga). Tia ot nằm trong góc xoyb). Tia oz nằm trong góc yotCâu 2: Cho n điểm trên đt d ( n _{in} N, n 2) và điểm O ko nằm trên d. Vẽ các tia gốc O đi qua mỗi điểm đã cho. Có tất cả bao nhiêu góc đỉnh O mà các cạnh là các tia đã vẽ ở hình trên.Câu 3: Cho hai tia ko đối nhau ox, oy. Kẻ thêm 5 tia khác nhau nằm giữa ox, oy. Hỏi cả 7 tia này tạo thành bao nhiêu góc.Câu 4: Hình 3 cho bt góc AOM 90°, góc BON 35°. Tính góc MON( tí mk...
Đọc tiếp
Câu 1: Cho góc xoy khác góc bẹt, tia oz nằm trong góc đó , chúng tỏ rằng
a). Tia ot nằm trong góc xoy
b). Tia oz nằm trong góc yot
Câu 2: Cho n điểm trên đt d ( n \(_{\in}\) N, n> 2) và điểm O ko nằm trên d. Vẽ các tia gốc O đi qua mỗi điểm đã cho. Có tất cả bao nhiêu góc đỉnh O mà các cạnh là các tia đã vẽ ở hình trên.
Câu 3: Cho hai tia ko đối nhau ox, oy. Kẻ thêm 5 tia khác nhau nằm giữa ox, oy. Hỏi cả 7 tia này tạo thành bao nhiêu góc.
Câu 4: Hình 3 cho bt góc AOM= 90°, góc BON= 35°. Tính góc MON
( tí mk vẽ hĩnh sau )
Câu 5: Trên đt xy lấy điểm O và trên cùng nửa mặt phẳng bờ là xy và gai tia oz và ot. Sao cho góc yot = 134° và góc xoz = 136°. Tính góc toz
Câu 6: cho góc xoy = 120° và điểm A trong góc xoy. Sao cho góc toa = 75° và điểm B ko nằm trong góc xoy, góc xoB = 135°. Chứng tỏ rằng ba điểm A,O,B thẳng hàng.
Câu 7: Cho góc xot = 80°. Vẽ tia oz nằm trong góc xot. Sao cho góc xoz = 60°. Vẽ tia phân giác oy của góc xot
a) Tính góc xot
b) chứng tỏ rằng oz là tia pg của góc yot
Hình vẽ bài 4
https://i.imgur.com/DIk0hDOh.jpg ( Thông cảm con bn viết hộ nên hơi xấu )
Đúng 0
Bình luận (0)
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề :
- Áp dụng một của thước và cạnh Ox, kẻ đường thẳng a theo lề kia
- Làm tương tự với đường thẳng b
- Gọi M là giao điểm của a và b, ta cso OM là tia phân giác của góc xOy
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy
(Gợi ý : Dựa vào bài tập 12 chứng minh các khoảng cách từ M đề Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai kề của chiếc thước) rồi áp dụng định lí 2)
Đọc tiếp
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề :
- Áp dụng một của thước và cạnh Ox, kẻ đường thẳng a theo lề kia
- Làm tương tự với đường thẳng b
- Gọi M là giao điểm của a và b, ta cso OM là tia phân giác của góc xOy
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy
(Gợi ý : Dựa vào bài tập 12 chứng minh các khoảng cách từ M đề Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai kề của chiếc thước) rồi áp dụng định lí 2)
Hướng dẫn :
Theo cách vẽ thì M cách đều hai cạnh Ox, Oy (cùng bằng khoảng cách 2 lề của chiếc thước
Vì M cách đều Ox, Oy nên theo định lí đảo M thuộc phân giác của ˆxOyxOy^ hay OM là phân giác của ˆ
Đúng 0
Bình luận (0)
Hình sau là thước có khoảng cách giữa hai lề song song với nhau bằng h. Để vẽ tia phân giác của góc xOy, ta áp một lề của thước vào cạnh Ox rồi kẻ đường thẳng a theo lề kia, sau đó làm tương tự với cạnh Oy ta kẻ được đường thẳng b. Vì sao giao điểm M của a và b nằm trên tia phân giác của góc xOy?
Đọc tiếp
Hình sau là thước có khoảng cách giữa hai lề song song với nhau bằng h. Để vẽ tia phân giác của góc xOy, ta áp một lề của thước vào cạnh Ox rồi kẻ đường thẳng a theo lề kia, sau đó làm tương tự với cạnh Oy ta kẻ được đường thẳng b. Vì sao giao điểm M của a và b nằm trên tia phân giác của góc xOy?
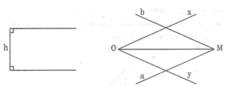
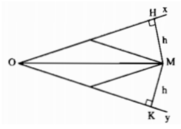
Kẻ MH ⊥ Ox, MK ⊥ Oy.
Khi đó:
MH là chiều rộng của thước hai lề
MK là chiều rộng của thước hai lề
Mà chiều rộng của thước đó bằng nhau và bằng h nên ta có:
MH = MK = h
Điểm M nằm trong góc xOy và cách đều hai cạnh của góc nên M thuộc tia phân giác của góc xOy.
Đúng 0
Bình luận (0)









