Cho tam giác đều ABC, O là một điểm bất kì nằm trong tam giác sao cho OA=8, OB=10, OC=12. Tìm AB

Những câu hỏi liên quan
Cho tam giác đều ABC, O là một điểm bất kì nằm trong tam giác sao cho OA=8, OB=10, OC=12. Tính AB
Cho tam giác đều ABC, O là điểm nằm trong tam giác sao cho OA=8, OB=10, OC=12. Tính AB
Đặt: \(AB=AC=BC=a\)
Độ dài a phải thoả mãn các bất đẳng thức trong tam giác:
\(\hept{\begin{cases}10-8< a< 10+8\\12-8< a< 12+8\\12-10< a< 12+10\end{cases}}\Leftrightarrow\hept{\begin{cases}2< a< 18\\4< a< 20\Leftrightarrow4< a< 18\left(\text{*}\right)\\2< a< 22\end{cases}}\)
\(\cos BAO=\frac{AO^2+AB^2-OB^2}{2.AO.AB}=\frac{a^2-36}{16a}\)
\(\cos CAO=\frac{AC^2+AO^2-OC^2}{2.AO.AB}=\frac{a^2-80}{16a}\)
Lại có:
\(\cos BAC=\cos\left(BAO+CAO\right)\)
\(\Leftrightarrow\cos60^o=\cos BAO.\cos CAO-\sin BAO.\sin CAO\)
\(\Leftrightarrow\frac{1}{2}=\cos BAO.\cos CAO-\sqrt{1-\cos^2BAO}.\sqrt{1-\cos^2CAO}\)
\(\Leftrightarrow\frac{1}{2}=\frac{a^2-36}{16a}.\frac{a^2-80}{16a}-\sqrt{1-\left(\frac{a^2-36}{16a}\right)^2}.\sqrt{1-\left(\frac{a^2-80}{16a}\right)^2}\)
\(\Leftrightarrow\frac{1}{2}=\frac{a^4-116a^2+2880}{256a^2}-\frac{\sqrt{\left(-a^4+328a^2-1296\right)\left(-a^4+416a^2-6400\right)}}{256a^2}\)
\(\Leftrightarrow128a^2=a^4-116a^2+2880-\sqrt{\left(-a^4+328a^2-1296\right)\left(-a^4+416a^2-6400\right)}\)
\(\Leftrightarrow\sqrt{\left(-a^4+328a^2-1296\right)\left(-a^4+416a^2-6400\right)}=a^4-244a^2+2880\) (1)
Điều kiện: \(a^4-244a^2+2880\ge0\left(\text{*}\text{*}\right)\)
\(\left(1\right)\Leftrightarrow a^8-744a^6+144144a^4-2638336a^2+8294400\)
\(=a^8+59536a^4+8294400-488a^6+5760a^4-1405440a^2\)
\(\Leftrightarrow256a^6-78848a^4+1232896a^2=0\)
\(\Leftrightarrow a^4-308a^2+4816=0\left(\Delta'=18900\Rightarrow\sqrt{\Delta'}=30\sqrt{21}\right)\)
\(\Leftrightarrow\orbr{\begin{cases}a^2=154+30\sqrt{21}\\a^2=154-30\sqrt{21}\end{cases}}\Rightarrow\orbr{\begin{cases}a=\sqrt{154+30\sqrt{21}}\left(\text{nhận}\right)\\a=\sqrt{154-30\sqrt{21}}\left(\text{loại vì không thoả }\left(\text{** }\right)\right)\end{cases}}\)
Vậy: \(AB=\sqrt{154+30\sqrt{21}}\)
Đúng 0
Bình luận (0)
Bổ sung cái thứ 2 thêm cái \(12-10< a< 12+10\) nữa , olm lưu thiếu hay mình viết thiếu k rõ nữa, tóm lại thêm cái đó vào nha ...
Đúng 0
Bình luận (0)
Cho tam giác ABC O là một điểm bất kì nằm trong tam giác chứng minh rằng 3 đoạn thẳng OA,OB,OC thỏa mãn bất đẳng thức tam giác
Cho tam giác đều ABC. O nằm bất kì trong tam giác ABC.CMR 3 đoạn OA,OB,OC đều thỏa mãn bất đẳng thức tong tam giác
3 đoạn thẳng OA,OB,OC thỏa mãn bất đẳng thức ta chứng minh
OA + OB > OC và OA - OB<OC .....
Trong tam giác AOB có OA + OB > AB => OA + OB > AC (1).
Do O nằm trong tam giác ABC => góc OAC < góc BAC => góc OAC < 60 độ
và góc OCA < góc BCA => góc OCA < 60 độ => góc AOC > 60 độ
trong tam giác AOC góc AOC lớn nhất => AC lớn nhất =>OC < AC (2)
từ (1) và (2) => OA + OB > OC tương tự ta có OB + OC > OA
=> OC > OA - OB hay OA-OB<OC....
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC đều, O bất kì nằm trong tam giác ABC. CMR: OA; OB; OC là độ dài 3 cạnh của một tam giác
- Chỉ cần nói cách vẽ thêm đường
Cho tam giác ABC có AB = BC = AC. Gọi O là một điểm bất kỳ nằm trong tam giác sao cho OA = OB = OC. Chứng minh rằng O là giao điểm 3 tia phân giác của các góc A; B; C.
Vì OA=OB=OC
nên O là tâm đường tròn ngoại tiếp ΔABC
mà ΔABC đều
nên O là giao điểm của ba tia phân giác của các góc A,B,C
Đúng 1
Bình luận (0)
Cho tam giác ABC có ABAC. Gọi E
∈
AC sao cho ABCE. Gọi O là một điểm nằm ở trong tam giác sao cho OAOC,OBOE. Khi đó: A.
Δ
A
O
B
Δ
C
E
O
B.
Δ
A
O
B
Δ
C
O
E
C.
A
O
B
^
O
E...
Đọc tiếp
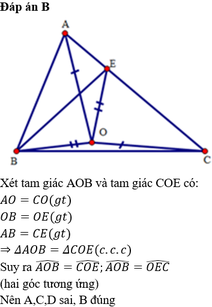
Cho tam giác ABC có AB<AC. Gọi E ∈ AC sao cho AB=CE. Gọi O là một điểm nằm ở trong tam giác sao cho OA=OC,OB=OE. Khi đó:
A. Δ A O B = Δ C E O
B. Δ A O B = Δ C O E
C. A O B ^ = O E C ^
D. A O B ^ = O E C ^
Cho tam giác ABC có AB=BC=AC.Gọi O là 1 điểm bất kì nằm trong tam giác sao cho OA=OB=OC.CMR O là giao điểm 3 tia phân giác của các góc A,B,C
Xét tam giác ABO và tam giác ACO
có AB=AC (GT
OA chung
OB=OC (GT)
suy ra tam giác ABO = tam giác ACO (c.c.c)
suy ra góc BAO=góc CAO
mà O nằm trong tam giác ABC nên tia AO nằm giữa hai tia AB và AC
suy ra AO là tia phân giác của góc BAC (1)
Chứng minh tương tự :BO là tia phân giác của góc ABC (2)
CO là tia phân giác của góc ACB (3)
Từ (1) , (2), (3) suy ra dpcm
gọi O là điểm bất kì nằm trong tam giác ABC. CMR:
a, OB+OC < AB+AC
b, OA+OB + OC > nửa chu vi nhung <chu vi cu tam giá ABC