a, Khi \(x = 0 ⇔ 0! + y! = y! ⇔ \) Vô lý.

\(\rightarrow x \ne y\)\(\ne 0\)

Khi \(x = y \rightarrow 2 . x! = (2x)! \rightarrow 2x! = x(x+1)(x+2)...(2x)=>x(x+1)(x+2)...(2x) = 2 \rightarrow x = y = 1. \)

Nếu \(x \ne y \rightarrow\) Vì vai trò của \(x,y\) là bình đẳng nên giả sử \(x < y\)

\(\rightarrow x!+y!<2.y!≤(y+1).y!=(y+1)!<(x+y)!\)

Vì \(x \ne y \ne 1 => (x+y) \ne (y+1) \rightarrow (x+y)! \ne (y+1).\)

Vậy \((x,y) = {(1,1)}.\)

b, Chứng minh bằng phương pháp phản chứng:

Giả sử \(x^{17} + y^{17} = 19^{17} \) có nghiệm nguyên.

Không mất tổng quát, giả sử \(x < y\)

\(\rightarrow x^{17} < y^{17} ≤ 19^{17}\)

\(\rightarrow (y+1)^{17} ≤ 19^{17} \)

\(\rightarrow y^{17} + 17y^{16} = 19^{17}\)

Mà \(\rightarrow x > 17 \rightarrow x = y =18.\)

Thử lại không đúng, suy ra giả sử sai.

\(\rightarrow\) Không tồn tại số nguyên thỏa mãn.

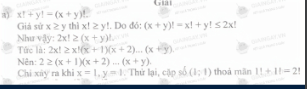
From : https://solvee.vn/r/baitap/812003032

giả sử: \(x^{17}+y^{17}=19^{17}\) và \(1\le x\le y\le19\)

Ta có: \(19^{17}\ge\left(y+1\right)^{17}\)

\(\Rightarrow19^{17}>y^{17}+17y^{16}\)

Vậy x>17, chỉ có thể x=y=18

Thử lại, x=y=18 không thoả 

Vậy pt đã cho không có nghiệm nguyên

 Bài 1: Bài này số nhỏ nên chỉ cần chặn miền giá trị của \(x\) rồi xét các trường hợp thôi nhé. Ta thấy \(3^x< 35\Leftrightarrow x\le3\). Nếu \(x=0\) thì \(VT=2\), vô lí. Nếu \(x=1\) thì \(VT=5\), cũng vô lí. Nếu \(x=2\) thì \(VT=13\), vẫn vô lí. Nếu \(x=3\) thì \(VT=35\), thỏa mãn. Vậy, \(x=3\).

 Bài 2: Nếu \(x=0\) thì pt đã cho trở thành \(0!+y!=y!\Leftrightarrow0=1\), vô lí,

Nếu \(x=y\) thì pt trở thành \(2x!=\left(2x\right)!\) \(\Rightarrow\left(x+1\right)\left(x+2\right)...\left(2x\right)=2\) \(\Leftrightarrow x=1\Rightarrow y=1\)

Nếu \(x\ne y\) thì không mất tính tổng quát, giả sử \(1< y< x\) thì \(x!+y!< 2x!\le\left(x+1\right)x!=\left(x+1\right)!< \left(x+y\right)!\) nên pt đã cho không có nghiệm trong trường hợp này.

Như vậy, \(x=y=1\)

 Bài 3: Bổ sung đề là pt không có nghiệm nguyên dương nhé, chứ nếu nghiệm nguyên thì rõ ràng \(\left(x,y\right)=\left(0,19\right)\) là một nghiệm cũa pt đã cho rồi.

Giả sử pt đã cho có nghiệm nguyên dương \(\left(x,y\right)\)

Khi đó \(x,y< 19\). Không mất tính tổng quát ta có thể giả sử \(1< y\le x< 19\). Khi ấy \(x^{17}+y^{17}=19^{17}\ge\left(x+1\right)^{17}=x^{17}+17x^{16}+...>x^{17}+17x^{16}\), suy ra \(y^{17}>17x^{16}\ge17y^{16}\) \(\Rightarrow y>17\). Từ đó, ta thu được \(17< y\le x< 19\) nên \(x=y=18\). Thử lại thấy không thỏa mãn. 

Vậy pt đã cho không có nghiệm nguyên dương.

Chị độc giải sau khi em biết làm thôi à.

`x^2-3y^2=17`

`<=>x^2=3y^2+17`

Vì `3y^2 vdots 3`

`17:3` dư 2

`=>3y^2+17:3` dư 2

`=>x^2:3` dư 2

Mà `x^2` là 1 số chính phương nên chia 3 dư 0 hoặc 1

Vậy phương trình vô nghiệm.

Dịt cụ mày

mày bị ngáo ak. đã xấu còn bị điên. đã bị điên cò học dốt

y^2+7=z

\(\Leftrightarrow x^2+4z=17\left(x^4+z^2\right)\)Hiển nhiên \(VP\ge VT\) đẳng thức chỉ xẩy ra khi x=z=0

với z=0=> y^2+7=0 vô nghiệm

KL vô nghiệm nguyên

What the fuck