Tính bằng cách thuận tiện
34x6+34x2+34x2/17x2x5
Tính bằng cách thuận tiện nhất:
34x6+34x2+34x2/17x2x5
=34x(6+2+2)x2/17x(2x5)
=34x10x2/17x10
=340x1.17647058824
=400.000000002
=34x(6+2+2)x2/17x(2x5)
=34x10x2/17x10
=340x1.17647058824
=400.000000002
=34x(6+2+2)x2/17x(2x5)
=34x10x2/17x10
=340x1.17647058824
=400.000000002
tính bằng cách thuận tiện nhất 34\33 x5\3 -34x2\3
Cho hàm số y = 3 4 x 2
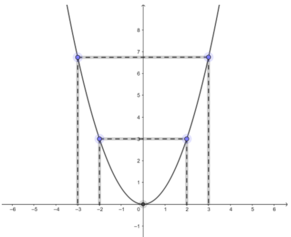
Tìm trên đồ thị các điểm có tung độ bằng 4. Tính gần đúng (làm tròn đến chữ số thập phân thứ nhất) hoành độ của những điểm này bằng hai cách :
- Ước lượng trên đồ thị ;
- Tính theo công thức y = 3 4 x 2
*Từ điểm có tung độ y = 4, kẻ đường thẳng song song với trục hoành cắt đồ thị hàm số tại hai điểm là B và B’. Cả hai điểm đều có tung độ y = 4.
Từ B và B’, kẻ hai đường thẳng song song với trục tung cắt trục hoành tại hai điểm có hoành độ lần lượt là x ≈ -2,3 và x ≈ 2,3.
*Thay y = 4 vào hàm số y = 3 4 x 2
ta có :
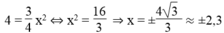
Tính lim x → + ∞ x + 3 4 x 2 + 1 - 2 ?
A. 1 4
B. 1 2
C. - 3 2
D. 0
½ nha học tốt
Tính tổng sau: 546,78+34x2+567,23+45,99=....
546,78 + 34 x 2 + 567,23 +45,99
= 614,78 + 613,22
=1228
Vậy kết quả là 1228
546.78+34x2+567.23+45.99=
1228 nha bn
Cho hàm số y = 3 4 x 2
Tìm trên đồ thị điểm A có hoành độ bằng -2. Bằng đồ thị, tìm tung độ của A.
Từ điểm có hoành độ x = -2, kẻ đường thẳng song song với trục tung cắt đồ thị tại điểm A. Từ A, kẻ đường thẳng song song với trục hoành cắt trục tung tại một điểm. Ta thấy điểm đó có tung độ y = 3.
Vậy A(-2 ; 3).
1,1+1,2x1,3x1,4x...x1,2011x(34x2-17x4):(2011-19x5+1890)
1,1 + 1,2\(\times\) 1,3 \(\times\) 1,4 \(\times\)...\(\times\) 1,2011\(\times\)(34\(\times\)2 - 17\(\times\)4):(2011-19\(\times\)5+1890)
=1,1 + 1,2 + 1,3 \(\times\)1,4 \(\times\)...\(\times\)1,2001\(\times\)(78 - 78):(2011 - 19\(\times\)5+1890)
= 1,1 +1,2 +1,3\(\times\)1,4\(\times\)...\(\times\)1,2001\(\times\)0:(2011-19\(\times\)5 + 1890)
= 1,1 + 0
= 1,1
1,1+1,2+1,3+.....1,2011x(68-68):(2011-19x5+1890)=1,1+1,2+1,3+...+1,2011x0:(2011-19x5+1890)=0
Giải phương trình: 2x4-21x3+34x2+105x+50=0.
Ta có: \(2x^4-21^3+34x^2+105x+50=0\)
\(\Leftrightarrow2x^4-12x^3-10x^2-9x^3+54x^2+45x-10x^2+60x+50=0\)
\(\Leftrightarrow2x^2\left(x^2-6x-5\right)-9x\left(x^2-6x-5\right)-10\left(x^2-6x-5\right)=0\)
\(\Leftrightarrow\left(x^2-6x-5\right)\left(2x^2-9x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-6x-5=0\\2x^2-9x-10=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3+\sqrt{14}\\x=3-\sqrt{14}\\x=\dfrac{9+\sqrt{161}}{4}\\x=\dfrac{9-\sqrt{161}}{4}\end{matrix}\right.\)