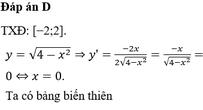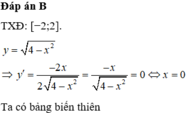Tìm GTNN và GTLN của 2m/(m2+1)

Những câu hỏi liên quan
Bài 1: Cho y=x2-4x (P)
a,Khảo sát sự biến thiên và vẽ đồ thị hàm số (P)
b,Tìm GTLN,GTNN của hàm số trên [0;4]
c,Tìm m để phương trình:x2-4x+2m=0 có 2 nghiệm phân biệt
Bài 2:Tìm m để GTNN của y=-x2+4x+m2-2m trên [-1;3] bằng 1
Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)
Đúng 1
Bình luận (0)
Bài 4: Cho PT sau : ( m2 + 1 ) x - 2m = 0 ( m là tham số)
a) CMR : PT là PT bậc nhất 1 ẩn với mọi n
b) Tìm m để nghiện của PT
- Đạt GTLN
- Đạt GTNN
Tìm GTLN và GTNN của: \(S=\dfrac{2m^2+7m+23}{m^2+2m+10}\) (m là tham số thực)
\(S=\dfrac{2m^2+7m+23}{m^2+2m+10}\Rightarrow Sm^2+2Sm+10S=2m^2+7m+23\)
\(\Leftrightarrow\left(S-2\right)m^2+\left(2S-7\right)m+10S-23=0\)
\(\Delta=\left(2S-7\right)^2-4\left(S-2\right)\left(10S-23\right)\ge0\)
\(\Leftrightarrow4S^2-16S+15\le0\)
\(\Rightarrow\dfrac{3}{2}\le S\le\dfrac{5}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(m=-4\)
\(S_{max}=\dfrac{5}{2}\) khi \(m=2\)
Đúng 1
Bình luận (2)
Tìm GTLN, GTNN của P=\(\frac{4m^2+2m+4}{m^2+1}\)
Tìm GTLN, GTNN của P=\(\frac{4m^2+2m+4}{m^2+1}\)
Gọi M và m lần lượt là GTLN và GTNN của hàm số
y
4
-
x
2
trên tập xác định. Khi đó
M
2
+
m
2
bằng A. 8 B. 16 C. 2 D. 4
Đọc tiếp
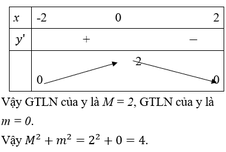
Gọi M và m lần lượt là GTLN và GTNN của hàm số y = 4 - x 2 trên tập xác định. Khi đó M 2 + m 2 bằng
A. 8
B. 16
C. 2
D. 4
Gọi M và m lần lượt là GTLN và GTNN của hàm số
y
4
−
x
2
trên tập xác định. Khi đó
M
2
+
m
2
bằng A. 2 B. 4 C. 16 D. 8
Đọc tiếp
Gọi M và m lần lượt là GTLN và GTNN của hàm số y = 4 − x 2 trên tập xác định. Khi đó M 2 + m 2 bằng
A. 2
B. 4
C. 16
D. 8
Tìm GTNN, GTLN của \(\frac{5-2m}{m^2+2}\)
Đặt \(A=\frac{5-2m}{m^2+2}\Leftrightarrow Am^2+2A-5+2m=0\)
\(\Leftrightarrow Am^2+2m+\left(2A-5\right)=0\)
Để \(PT\) trên có nghiệm \(\Leftrightarrow\Delta'=1-A\left(2A-5\right)=-2A^2+5A+1\ge0\)
\(\Leftrightarrow\frac{5-\sqrt{33}}{4}\le A\le\frac{5+\sqrt{33}}{4}\)
Kết quả ko đẹp lắm nếu cảm thấy sai thì bạn lại đề; mình giải ko sai đâu
Đúng 0
Bình luận (0)
Bài 1: Tìm GTNN và GTLN của \(A=123+\sqrt{-x^2+6x+5}\)
Bài 2:Tìm GTNN và GTLN của \(A=\sqrt{-x^2+8x-12}-7\)
Bài 3: Tìm GTNN và GTLN của \(A=\sqrt{-x^2-x+4}\)