Cho hình thang MNPQ có đáy nhỏ MN=4cm, đáy lớn PQ= 6cm . Khi đó độ dài đường trung bình của hình thang MNPQ là... cm
Cho hình thang MNPQ có đáy nhỏ MN=4cm, đáy lớn PQ= 6cm . Khi đó độ dài đường trung bình của hình thang MNPQ là... cm
đường trung bình hình thang MNPQ = (6+4):2 = 5 (cm)
mik nha chế
Cho hình thang có đáy nhỏ
, đáy lớn
. Khi đó độ dài đường trung bình của hình thang
là cm
Ta có : GỌi dộ dài đường trung bình là EF
=> EF=(MN+PQ):2=(4+6):2=10:2=5
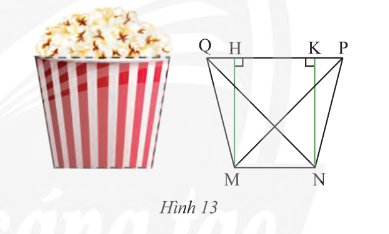
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
cho hình thang cân MNPQ có độ dài cạnh đáy là MN = 7cm, độ dài cạnh đáy PQ gấp đôi độ dài cạnh đáy MN , độ dài chiều cao MH= 4cm.Tính diện tích hình thang cân ABCD?
PQ=7*2=14cm
\(S_{MNPQ}=\dfrac{1}{2}\cdot\left(7+14\right)\cdot4=2\cdot21=42\left(cm^2\right)\)
Cho hình thang cân ABCD có đáy lớn DC = 7cm; góc C = 60độ, BC = 4cm . Độ dài đường trung bình MN của hình thang ABCD là __ cm
Tk
Kẻ BE là phân giác ˆABCABC^.
ΔBECΔBEC đều →BE=EC=BC=4→BE=EC=BC=4
Do AB//DE;AD//BEAB//DE;AD//BE nên AB=DE=DC−EC=7−4=3AB=DE=DC−EC=7−4=3
MN là đường trung bình của hình thang ABCD →MN=AB+CD2→MN=AB+CD/2
⟺MN=3+7/2=5
tk
MN = 5cm
cách tính thì tính cạnh AB = 3m , thui nói nhiều làm chi ghi đáp án = 5
Cho hình thang cân MNPQ (MN // PQ) có góc M Q P ^ = 45 ° và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
A. 728 c m 2 .
B. 346 c m 2 .
C. 364 c m 2 .
D. 362 c m 2 .
Đáp án cần chọn là: C
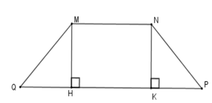
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 12 cm nên QH = KP = 40 − 12 2 = 14 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 12 + 40 ) .14 2 = 364 c m 2
Cho hình thang cân MNPQ (MN // PQ) có góc M Q P ^ = 45 ° và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
A. 418 c m 2 .
B. 209 c m 2
C. 290 c m 2 .
D. 580 c m 2 .
Đáp án cần chọn là: B
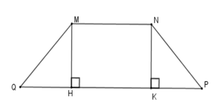
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 8 cm nên QH = KP = 30 − 8 2 = 8 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 8 + 30 ) .11 2 = 209 c m 2 .
Cho hình thang MNPQ, có đáy bé MN bằng 3/5 đáy lớn PQ. Hai đường chéo MP và NQ cắt nhau tại K. Biết diện tích tam giác NPK là 15cm2. Tính diện tích hình thang MNPQ.
Lời giải:
$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)
$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm2)
Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$
\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)
\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)
\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)
Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$
$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$
$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm2)
$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$
$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm2)
Diện tích hình thang:
$15+15+9+25=64$ (cm2)
Cho hình thang MNPQ với đáy lớn là PQ, đáy nhỏ là MN. E là trung điểm MP CMR: các vectơ EM+EN+EP+EQ=PN+MQ
\(\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}+\overrightarrow{EQ}\)
\(=\overrightarrow{EN}+\overrightarrow{EQ}\)(1)
\(\overrightarrow{PN}+\overrightarrow{MQ}\)
\(=\overrightarrow{PE}+\overrightarrow{EN}+\overrightarrow{ME}+\overrightarrow{EQ}\)
\(=\overrightarrow{EN}+\overrightarrow{EQ}\)(2)
Từ (1) và (2) suy ra \(\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}+\overrightarrow{EQ}=\overrightarrow{PN}+\overrightarrow{MQ}\)