Trên mặt phẳng cho 11 đường thẳng cắt nhau từng đôi một . CMR : Luôn luôn có 1 góc tạo thành nhỏ hơn 17 độ

Những câu hỏi liên quan
trên mặt phẳng cho 4 đường thẳng cắt nhau từng đôi một . chúng tạo thành bao nhiêu góc
giúp với
Trên mặt phẳng cho 7 đường thẳng, chúng cắt nhau từng đôi một và không có 3 đường thẳng nào đồng quy.
a) Có bao nhiêu giao điểm?
b) Có bao nhiêu tia được tạo thành?
c) Có bao nhiêu góc được tạo thành?
d) Chia mặt phẳng thành bao nhiêu phần?
1. Qua điểm A nằm ngoài đường thẳng a , vẽ 60 đường thẳng phân biệt . Hỏi có ít nhất bao nhiêu đường thẳng cắt a ?2. Qua điểm O vẽ 5 đường thẳng phân biệt .Hỏi có bao nhiêu cặp góc đối đỉnh . Nếu chỉ xét các góc không có điểm trong chung thì luôn tồn tại một góc nhỏ hơn bao nhiêu độ ?3. Qua điểm O vẽ n đường thẳng phân biệt .Muốn có 4950 góc thì phải vẽ bao nhiêu đường thẳng ?4. Cho 5 đường thẳng phân biệt không có 2 đường thẳng nào song song . CMR trong các góc tạo thành luôn có ít nhất một góc...
Đọc tiếp
1. Qua điểm A nằm ngoài đường thẳng a , vẽ 60 đường thẳng phân biệt . Hỏi có ít nhất bao nhiêu đường thẳng cắt a ?
2. Qua điểm O vẽ 5 đường thẳng phân biệt .Hỏi có bao nhiêu cặp góc đối đỉnh . Nếu chỉ xét các góc không có điểm trong chung thì luôn tồn tại một góc nhỏ hơn bao nhiêu độ ?
3. Qua điểm O vẽ n đường thẳng phân biệt .Muốn có 4950 góc thì phải vẽ bao nhiêu đường thẳng ?
4. Cho 5 đường thẳng phân biệt không có 2 đường thẳng nào song song . CMR trong các góc tạo thành luôn có ít nhất một góc nhỏ hơn hoặc bằng 36 độ .
trên mặt phẳng cho 2012 đường thẳng từng đôi một cắt nhau có tính chất qua giao điểm của 2 đường thẳng bất kì có thêm 1 đường thẳng nữa đi qua. CMR 2012 đường thẳng đồng quy
Bài 1: Cho góc xoy=150 độ vẽ tia oz là tia phân giác của góc xoy, tia oa là tia đối tia oz. Tính góc yoz, aoy
Bài 2: Cho đỉnh O thuộc đường thẳng AB, trên cùng nửa mặt phẳng bờ ab vẽ 3 tia om, on, oe
a, Kể tên các góc kều bù
b, CMR: Trong các góc tạo thành luôn tồn tại một góc nhỏ hơn hoặc bằng 45 độ
Giúp mình với cảm ơn nhiều ạ
Cho hai đường thẳng chéo nhau
∆
và
∆
′ có AA’ là đoạn vuông góc chung, trong đó A
∈
∆
và A′
∈
∆
′. Gọi (
α
) là mặt phẳng chứa AA’ và vuông góc với
∆
′ và cho biết AA’ a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng (
α
) lần lượt cắt
∆
và ...
Đọc tiếp
Cho hai đường thẳng chéo nhau ∆ và ∆ ′ có AA’ là đoạn vuông góc chung, trong đó A ∈ ∆ và A′ ∈ ∆ ′. Gọi ( α ) là mặt phẳng chứa AA’ và vuông góc với ∆ ′ và cho biết AA’ = a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng ( α ) lần lượt cắt ∆ và ∆ ′ tại M và M’ . Hình chiếu vuông góc của M trên mặt phẳng ( α ) là M 1 . Chứng minh rằng khi x thay đổi mặt cầu tâm O luôn luôn chứa một đường tròn cố định.
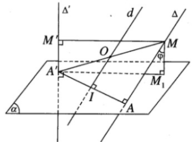
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.
Đúng 0
Bình luận (0)
Trên một mặt phẳng,cho 7 đường thẳng trong đó không có hai đường thẳng nào song song.Chứng minh có ít nhất hai đường thẳng cắt nhau theo một góc nhỏ hơn 60 độ.
Cho 5 đường thẳng đôi một cắt nhau.CMR trong số các góc tạo thành của 2 đường thẳng trong 5 đường thẳng đã cho,luôn tồn tại một góc có số đo không vượt quá 36 độ.
Ta chọn điểm O bất kì nằm trong mặt phẳng chứa 5 đường thẳng ấy. Qua O ta dựng các đường thẳng song song với các đường thẳng đã cho , khi đó có 10 góc đôi một đối đỉnh qua O . Vậy sẽ có ít nhất một góc không vượt quá \(\frac{180^o}{5}=36^o\)
Đúng 0
Bình luận (0)
Trên cùng một nửa mặt phẳng cho 7 đường thẳng phân biệt trong đó không có 2 đường thẳng nào song song.
CMR:Ít nhất có 2 đường thẳng cắt nhau theo 1 góc nhỏ hơn 26 độ












