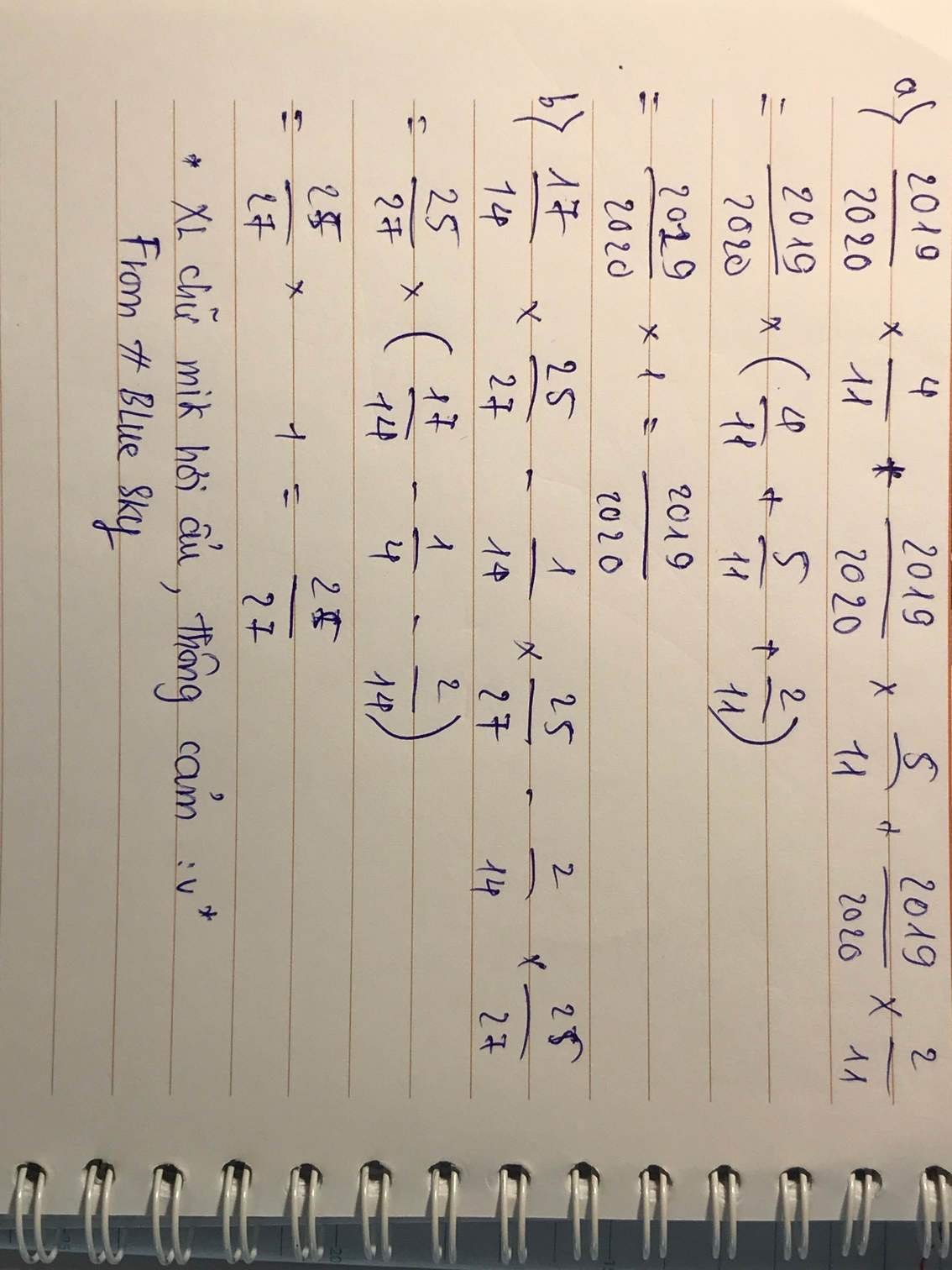hì...mơn anh

thiếu 1 số chỗ đó

 cứ thấy sai sai chỗ nào ý

\(a.=\dfrac{2019}{2020}\times\left(\dfrac{4}{11}+\dfrac{5}{11}+\dfrac{2}{11}\right)\\ =\dfrac{2019}{2020}\times1=\dfrac{2019}{2020}\\ b.=\dfrac{25}{27}\times\left(\dfrac{17}{14}-\dfrac{1}{14}-\dfrac{2}{14}\right)\\ =\dfrac{25}{27}\times1=\dfrac{25}{27}\)

Thanks mik chữ cũng hơi ẩu

( - 2019 - 2019 - 2019 - 2019 ) x ( -25 ) 

= (-4 ) x 2019 x ( - 25 ) 

= ( -4 ) x ( -25 ) 2019 

= 100 x 2019 

= 201900 

học tốt 

201900

26 x 84 + 74 x 85

= 26 x 84 + 74 x 84 + 74

= 84 x (26 + 74) + 74

= 84 x 100 + 74

= 840 + 74

= 914

\(\frac{2017\times2018+2019}{2019\times2018-2017}\)

= \(\frac{2019\times2018-2\times2018+2019}{2019\times2018-2017}\)

= \(\frac{2019\times2018-4036+2019}{2019\times2018-2017}\)

= \(\frac{2019\times2018-2017}{2019\times2018-2017}\)

= 1

dung may tinh la duoc roi

Dùng máy tính đó

Hoặc động cái não mà nghĩ đi với

nhân chia trước cộng trừ sau
cứ thế mà tính

nhanh nhanh các bạn ơi

26x84+74x85=8474

2017x2018+2019/2019x2018-2017=4070307

câu trả lời đấy cu

Lời giải:

$x:0,1+x:0,5-x:25\text{%}+x+x=2019$

$x\times 10+x\times 2-x\times 4+x+x=2019$

$x\times (10+2-4+1+1)=2019$

$x\times 10=2019$

$x=2019:10=201,9$

Đáp án A.

khó

Lời giải:

$x:0,1+x:0,5-x:25\text{\%}+x+x=2019$

$x\times 10+x\times 2-x\times 4+x+x=2019$

$x\times (10+2-4+1+1)=2019$

$x\times 10=2019$

$x=2019:10=201,9$

Đáp án A.

Lời giải:
Đặt \(\frac{x}{a}=m; \frac{y}{b}=n; \frac{z}{c}=p\). Khi đó:

ĐKĐB $\Leftrightarrow \frac{a^2m^2+b^2n^2+c^2p^2}{a^2+b^2+c^2}=m^2+n^2+p^2$

$\Rightarrow a^2m^2+b^2n^2+c^2p^2=(a^2+b^2+c^2)(m^2+n^2+p^2)$

$\Leftrightarrow a^2n^2+a^2p^2+b^2m^2+b^2p^2+c^2m^2+c^2n^2=0$
$\Rightarrow an=ap=bm=bp=cm=cn=0$

Vì $a,b,c\neq 0$ nên $m=n=p=0$

$\Rightarrow x=y=z=0$

Khi đó:

$\frac{x^{2019}+y^{2019}+z^{2019}}{a^{2019}+b^{2019}+c^{2019}}=0$

$\frac{x^{2019}}{a^{2019}}=\frac{y^{2019}}{b^{2019}}=\frac{z^{2019}}{c^{2019}}=0$

$\Rightarrow$ đpcm

Vì \(x=2018\Rightarrow x+1=2019\)

Thay x+1=2019 vào biểu thức A  ta được :

\(A=x^6-\left(x+1\right)x^5+\left(x+1\right)x^4-...-\left(x+1\right)x+x+1\)

\(=x^6-x^6-x^5+x^5+x^4-...-x^2-x+x+1\)

\(=1\)

\(A=x^6-2019x^5+2018x^4-2019x^3+2019x^2-2019x+2019\)

\(=x^6-2018x^5-x^5+2018x^4+x^4-2018x^3-x^3+2018x^2+x^2\)

\(-2018x-x+2019\)

\(=x^5\left(x-2018\right)-x^4\left(x-2018\right)-x^3\left(x-2018\right)+x^2\left(x-2018\right)\)

\(+x\left(x-2018\right)-\left(x-2018\right)+1\)

= 1

Vì \(x=2018\Rightarrow x+1=2019\)

Thay \(x+1=2019\) vào biểu thức \(A\) ta được :

\(A=x^6-\left(x+1\right)x^5+\left(x+1\right)x^4-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+\left(x-1\right)\)

\(=x^6-x^6-x^5+x^5-x^4+x^4-x^3+x^3-x^2+x^2-x+x+1\)

\(=1\)

ĐKXĐ: \(\left\{{}\begin{matrix}a\ne0\\b\ne0\\c\ne0\end{matrix}\right.\)Ta có: \(\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}\)

\(\Leftrightarrow\left(a^2+b^2+c^2\right)\cdot\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}=\left(a^2+b^2+c^2\right)\cdot\left(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}\right)\)

\(\Leftrightarrow x^2+y^2+z^2=x^2+\dfrac{x^2\cdot\left(b^2+c^2\right)}{a^2}+y^2+\dfrac{y^2\left(a^2+c^2\right)}{b^2}+z^2+\dfrac{z^2\cdot\left(a^2+b^2\right)}{c^2}\)

\(\Leftrightarrow x^2\cdot\dfrac{b^2+c^2}{a^2}+y^2\cdot\dfrac{a^2+c^2}{b^2}+z^2\cdot\dfrac{a^2+b^2}{c^2}=0\)(1)

Vì (1) luôn không âm mà a,b,c≠0

nên x=y=z=0

⇒\(\dfrac{x^{2019}+y^{2019}+z^{2019}}{a^{2019}+b^{2019}+c^{2019}}=\dfrac{0^{2019}+0^{2019}+0^{2019}}{a^{2019}+b^{2019}+c^{2019}}=0\)

mà \(\dfrac{x^{2019}}{a^{2019}}+\dfrac{y^{2019}}{b^{2019}}+\dfrac{z^{2019}}{c^{2019}}=\dfrac{0^{2019}}{a^{2019}}+\dfrac{0^{2019}}{b^{2019}}+\dfrac{0^{2019}}{c^{2019}}=0\)

nên \(\dfrac{x^{2019}+y^{2019}+z^{2019}}{a^{2019}+b^{2019}+c^{2019}}=\dfrac{x^{2019}}{a^{2019}}+\dfrac{y^{2019}}{b^{2019}}+\dfrac{z^{2019}}{c^{2019}}\)