5.

\(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ac}+\sqrt{ab}\)

\(\Rightarrow\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\dfrac{a}{a+\sqrt{ac}+\sqrt{ab}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)

Tương tự:

\(\dfrac{b}{b+\sqrt{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)

\(\dfrac{c}{c+\sqrt{\left(a+c\right)\left(b+c\right)}}\le\dfrac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)

Cộng vế với vế:

\(P\le\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1\)

Dấu "=" xảy ra khi \(a=b=c\)

6.

\(P=\dfrac{a}{1+b-a}+\dfrac{b}{1+c-b}+\dfrac{c}{1+a-c}\)

Thay \(1=a+b+c\)

\(\Rightarrow P=\dfrac{a}{2b+c}+\dfrac{b}{2c+a}+\dfrac{c}{2a+b}\)

\(P=\dfrac{a^2}{2ab+ac}+\dfrac{b^2}{2bc+ab}+\dfrac{c^2}{2ac+bc}\)

\(P\ge\dfrac{\left(a+b+c\right)^2}{3ab+3bc+3ca}\ge\dfrac{3\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}=1\)

Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)

7.

\(T=\left(x^2\right)^2+\left(y^2\right)^2+\left(z^2\right)^2\ge\dfrac{1}{3}\left(x^2+y^2+z^2\right)^2\)

\(T\ge\dfrac{1}{3}\left(xy+yz+zx\right)^2=\dfrac{1}{3}\)

\(T_{min}=\dfrac{1}{3}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)

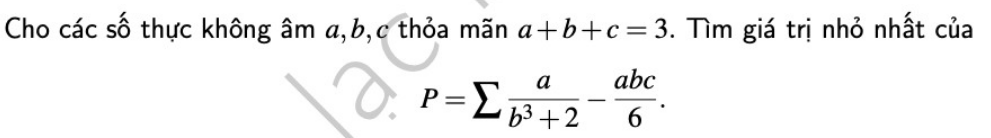
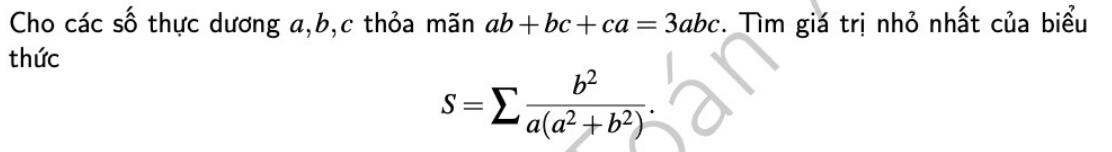
Thầy Nguyễn Việt Lâm ơi giúp em mấy bài này với.Em sắp phải nộp rồi ạ  - Hoc24

học đi bạn ey !

học đi bạn eiii.

đừng lao đầu vào facebook nha!!

chúc bạn học giỏi!!

I. Rules of paripation "Help me solve maths" 1. Don't put miscellaneous questions on the forum, only post arles that you can't solve or good questions on the forum; 2. Do not answer miscellaneous, does not match the question content on the forum. 3. Do not "True" on miscellaneous answers to fraud points. Those who violate the 3 above will be deducted from all questions by Online Math teachers, may be locked out of the account or permanently banned from logging in to the website.

xin xong roi anh hai nguoi giong nhau ha

dien moi cho

đc ok FB MIK Là Vương Tôn

nguyễn bảo trân ns j đấy hả. mk k hiểu

TDT là j tek bạn

https://www.facebook.com/profile.php?id=100027537114284

I. Nội qui tham gia "Giúp tôi giải toán"

1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;

2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.

3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.

Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

4.

\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)

Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)

\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)

\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)

\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)

5.

Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)

Đặt vế trái là P

\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)

Quay lại dòng 3 của bài số 4

6.

Do a;b;c không âm, ta có:

\(b^2\left(b-1\right)^2\left(b+2\right)\ge0\)

\(\Leftrightarrow b^5-3b^3+2b^2\ge0\)

\(\Leftrightarrow b^5-3b^3+2b^2-6\ge-6\)

\(\Leftrightarrow-\left(3-b^2\right)\left(b^3+2\right)\ge-6\)

\(\Leftrightarrow6\ge\left(3-b^2\right)\left(b^3+2\right)\)

\(\Rightarrow\dfrac{1}{b^3+2}\ge\dfrac{3-b^2}{6}\)

\(\Rightarrow\dfrac{a}{b^3+2}\ge\dfrac{a\left(3-b^2\right)}{6}\)

Tương tự: \(\dfrac{b}{c^3+2}\ge\dfrac{b\left(3-c^2\right)}{6}\) ; \(\dfrac{c}{a^3+2}\ge\dfrac{c\left(3-a^2\right)}{6}\)

Cộng vế: \(P\ge\dfrac{a+b+c}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}=\dfrac{3}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}\)

Không mất tính tổng quát, giả sử \(b=mid\left\{a;b;c\right\}\)

\(\left(b-a\right)\left(b-c\right)\le0\)

\(\Leftrightarrow b^2+ac\le ab+bc\)

\(\Leftrightarrow ab^2+ca^2\le a^2b+abc\)

\(\Rightarrow ab^2+bc^2+ca^2+abc\le bc^2+a^2b+2abc=b\left(a+c\right)^2=4b\left(\dfrac{a+c}{2}\right)\left(\dfrac{a+c}{2}\right)\le\dfrac{4}{27}\left(a+b+c\right)^3=4\)

\(\Rightarrow P\ge\dfrac{3}{2}-\dfrac{4}{6}=\dfrac{5}{6}\)

nha các bn

Nguyễn Quang Sáng là một nhà văn nổi tiếng và cũng là một nhân vật có nhiều câu chuyện thú vị xoay quanh cuộc đời và sự nghiệp của ông. Một câu chuyện thú vị về Nguyễn Quang Sáng là khi ông bị bắt giam vì viết những bài viết chính trị phản đối chính quyền cộng sản.

Trong thời gian bị giam, Nguyễn Quang Sáng không ngừng viết và gửi những bài viết của mình ra ngoài để thế giới biết về tình hình tù đày và cuộc sống của người dân Việt Nam. Ông đã sử dụng những phương pháp sáng tạo để truyền thông tin, bằng cách viết trên giấy vệ sinh, gấu búp bê, hoặc gửi qua những người thân đến thăm ông.

Câu chuyện này thể hiện sự kiên nhẫn, sáng tạo và tinh thần không khuất phục của Nguyễn Quang Sáng trong việc đấu tranh cho tự do ngôn luận và quyền con người.

chưa thi à ?