cho tam giác abc (ab < ac) nội tiếp đường tròn (o;r), m là trung điển của bc, tia oa cắt đường tròn (o) tại k ( k khác a ) đường cao cc' và bb' cắt nhau tại h. a) chứng minh m,h,k thẳng hàng b) Chứng minh om = 1/2 ah

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.
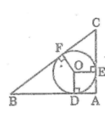
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
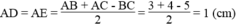
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn và ABAC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của widehat{MDC}c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh AB^2+AC^2+CD^2+BD^28R^2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
b) Chứng minh DA là tia phân giác của \(\widehat{MDC}\)
c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
d) Chứng minh \(AB^2+AC^2+CD^2+BD^2=8R^2\)
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
Đúng 0
Bình luận (0)
cho tam giác ABC nội tiếp đường tròn O,đường tròn K tiếp xúc trong vs đtròn O tại T và tiếp xúc 2 cạnh AB,AC tại E,F chưng minh tâm I đtròn nội tiếp tam giác ABC là trung điểm EF
Bổ sung: ΔABC cân tại A
ΔABC cân tại A
=>AO đi qua trug diểm I của EF
Vẽ IK vuông góc AB tại K, gọi H và G lần lượt là giao của OA với BC và(O)
Vì OE vuông góc AB, IK vuông goc AB, GB vuông góc AB
=>OE//IK//GB
ΔABG có IK//GB
nên IK/BG=AI/AG
=>IK=AI*BG/AG
ΔABH có EI//BH
ΔABE có OE//BG
=>IH/AH=BE/BA=OG/AG và AE/AB=AI/AH
=>IH=AH*OE/AE
ΔABG có OE//BG
nên AB/AE=BG/OE
AH/AI=AB/AE=BG/OE
=>AH*OE=AI*BG
=>AH*OG=AI*BG
=>IK=IH
=>ĐPCM
Đúng 0
Bình luận (1)
Cho tam giác ABC có AB=AC nội tiếp đường tròn tâm O, đường cao AH của tam giác cắt đường tròn O tại D
Cho tam giác ABC có 3 góc nhọn , ABC75 độ , (abac, ac cố định ) nội tiếp đường tròn tâm o . các đường cao AF và CE của tam giác abc cắt nhau tại h ( f thuộc bc , e thuộc ab ) a cm tứ giác BEHF nội tiếp b kẻ đường kính ak của đường tròn o .chứng minh ; hai tam giác abk và afc đồng dạng c khi b di chuyển trên cung lớn ac thì điểm H di chuyển trên đường nào giúp mình câu c ạ !!!
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn , ABC=75 độ , (ab<ac, ac cố định ) nội tiếp đường tròn tâm o . các đường cao AF và CE của tam giác abc cắt nhau tại h ( f thuộc bc , e thuộc ab )
a cm tứ giác BEHF nội tiếp
b kẻ đường kính ak của đường tròn o .chứng minh ; hai tam giác abk và afc đồng dạng
c khi b di chuyển trên cung lớn ac thì điểm H di chuyển trên đường nào
giúp mình câu c ạ !!!
Cho tam giác ABC có 3 góc nhọn , ABC75 độ , (abac, ac cố định ) nội tiếp đường tròn tâm o . các đường cao AF và CE của tam giác abc cắt nhau tại h ( f thuộc bc , e thuộc ab ) a cm tứ giác BEHF nội tiếp b kẻ đường kính ak của đường tròn o .chứng minh ; hai tam giác abk và afc đồng dạng c khi b di chuyển trên cung lớn ac thì điểm H di chuyển trên đường nào giúp mình câu c với ạ !!!
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn , ABC=75 độ , (ab<ac, ac cố định ) nội tiếp đường tròn tâm o . các đường cao AF và CE của tam giác abc cắt nhau tại h ( f thuộc bc , e thuộc ab )
a cm tứ giác BEHF nội tiếp
b kẻ đường kính ak của đường tròn o .chứng minh ; hai tam giác abk và afc đồng dạng
c khi b di chuyển trên cung lớn ac thì điểm H di chuyển trên đường nào
giúp mình câu c với ạ !!!
a: góc BEH+góc BFH=90 độ
=>BEHF nội tiếp
b: góc ABK=1/2*sđ cung AK=90 độ
Xét ΔABK vuông tại B và ΔAFC vuông tại F có
góc AKB=góc ACF
=>ΔABK đồng dạng với ΔAFC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB,AC lần lượt tại D và E.
Biết AB=3,AC=4cm.Bán kính đường tròn (O) là ......cm
Ta có: AC = 5
Gọi bán kính đường tròn nội tiếp là r
Ta có:
S(ABC) =S(OAB) + S(OAC) +S(OBC) (1)
S(OAB) = r*AB/2
S(OAC) = r*AC/2
S(OBC) = r*BC/2
=> S(OAB) + S(OAC) +S(OBC) = r* (AB+BC+CA)/2 = 6r (2)
Mặt khác; S(ABC) = AB.AC/2 = 6 (3)
Từ (1), (2), (3) :
=> 6r = 6 => r = 1.
Ủng hộ mk nha!
Đúng 0
Bình luận (0)
Cho tam giác $ABC$ vuông tại $A$. Đường tròn $(O)$ nội tiếp tam giác $ABC$ tiếp xúc với $AB$, $AC$ lần lượt tại $D$ và $E$.
a) Tứ giác $ADOE$ là hình gì?
b) Chứng minh \(S=p.r\) ($p$ là nửa chu vi tam giác $ABC$, $r$ là bán kính đường tròn nội tiếp).
b) Tính bán kính của đường tròn $(O)$ biết $AB = 6cm$, $AC = 8cm$.
BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr ( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).
giải:
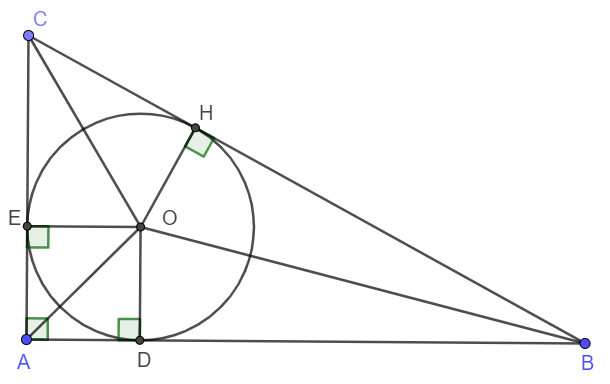
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có
( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: .
Diện tích tam giác ABC là: .
Chu vi tam giác ABC là: .
Suy ra: .
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A.Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB,AClần lượt tại D và E. Biết AB=3 cm,AC=4cTính bán kính đường tròn (O)
Cho tam giác ABC nhọn (ABAC) nội tiếp đường tròn (O). Gọi H là giao điểm của hai đường cao BE và CF, AD của tam giác ABC ( NAB, MAC )a) Chứng minh tứ giác BCEF nội tiếp đường tròn và AO vuông góc EFb) Kẻ đường kính AK của đường tròn (O). Chứng minh AD.AK AB. AC c) Đường thẳng EF cắt đường tròn (O) tại N và M ( E nằm giữa F và M ).Chứng minh AN là tiếp tuyến của đường tròn ngoại tiếp tam giác NHD
Đọc tiếp
Cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn (O). Gọi H là giao điểm của hai đường cao BE và CF, AD của tam giác ABC ( N![]() AB, M
AB, M![]() AC )
AC )
a) Chứng minh tứ giác BCEF nội tiếp đường tròn và AO vuông góc EF
b) Kẻ đường kính AK của đường tròn (O). Chứng minh AD.AK = AB. AC
c) Đường thẳng EF cắt đường tròn (O) tại N và M ( E nằm giữa F và M ).Chứng minh AN là tiếp tuyến của đường tròn ngoại tiếp tam giác NHD
a: Xét tứ giác BCEF có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BCEF là tứ giác nội tiếp đường tròn đường kính BC
Kẻ tiếp tuyến Ax của (O)
=>Ax\(\perp\)OA tại A
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AEF}\left(=180^0-\widehat{FEC}\right)\)
nên \(\widehat{xAC}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//FE
ta có: Ax//FE
OA\(\perp\)Ax
Do đó: OA\(\perp\)FE
b: Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó: ΔACK vuông tại C
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AKC}\)
Xét ΔADB vuông tại D và ΔACK vuông tại C có
\(\widehat{ABD}=\widehat{AKC}\)
Do đó: ΔADB~ΔACK
=>\(\dfrac{AD}{AC}=\dfrac{AB}{AK}\)
=>\(AD\cdot AK=AB\cdot AC\)
Đúng 0
Bình luận (0)



















