a) Số chia hết cho 2 là các số có chữ số tận cùng là 0; 2; 4; 6; 8. 

Do đó các chữ số thích hợp ở dấu * để số 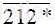 chia hết cho 2 là 0; 2; 4; 6; 8.

b) Số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5. 

Do đó các chữ số thích hợp ở dấu * để số 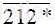 chia hết cho 5 là: 0; 5. 

c) Số chia hết cho cả 2 và 5 có chữ số tận cùng là 0 

Do đó các chữ số thích hợp ở dấu * để số 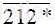 chia hết cho cả 2 và 5 là: 0.

a: 0;2;4;6;8

b: 5;0

c: 0

So can tim:47

Bài 1:

a) chữ số tận cùng = 3

b) Chữ số tận cùng =7

Gọi số đó là \(\overline{ab}\)(0<a<10; b<10)

Vì 58-9-9=40 nên số đó có dạng \(\overline{4b}\)hoặc \(\overline{5b}\)

                                      \(\Rightarrow\overline{4b}+4+b=58\)

                                  \(40+b+4+b=58\)

                                                  \(44+2b=58\)

                                                              \(2b=58-44\)

                                                              \(2b=14\)

                                                                 \(b=14:2\)

                                                                 \(b=7\)

-> \(\overline{ab}=47\)

                                                \(\Rightarrow\overline{5b}+5+b=58\)

                                            \(50+b+5+b=58\)

                                                            \(55+2b=58\)

                                                                        \(2b=58-55\)

                                                                        \(2b=3\)

Vì 3 không chia hết cho 2 nên ta không tìm được b thoả mãn trong trường hợp này

Vậy, số đó là 47

Thử lại: 47+4+7=58 (đúng)

Bạn tham khảo bài sau nhé:

https://hoidap247.com/cau-hoi/2044248