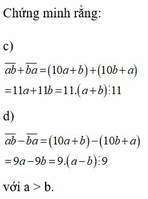chứng minh ab+ba chia hết cho 11

Những câu hỏi liên quan
Chứng minh rằng:
a) a b ¯ + b a ¯ chia hết cho 11.
b) a b ¯ - b a ¯ chia hết cho 9 với a > b.
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
Đúng 2
Bình luận (0)
Chứng minh rằng:
a, a b + b a chia hết cho 11
b, a b - b a chia hết cho 9 với a > b
a, a b + b a = (10a+b)+(10b+a) = 11a+11b = 11.(a+b) ⋮ 11
b, a b - b a = (10a+b) - (10b+a) = 9a - 9b = 9(a - b) ⋮ 9 (a>b)
Đúng 0
Bình luận (0)
Chứng minh:
1) (ab+ba) chia hết cho 11
2) (ab-ba) chia hết cho 9
1. ab+ba
= 10a+b+10b+a
= 11a+11b
= 11(a+b) chia hết cho 11
2. ab-ba
= 10a+b-(10b+a)
= 10a+b-10b-a
= 9a-9b
= 9(a-b) chia hết cho 9
Đúng 0
Bình luận (0)
a) ab = 10a + b
ba = 10b + a
=>ab + ba = 11(a+b) chia het cho 11.
b)ab=10a+b
ba=10b+a
ab-ba=9a-9b=9(a-b)=> ab-ba chia hết cho 9
Đúng 0
Bình luận (0)
chứng minh rằng abcabe chia hết cho 11
chứng minh ab-ba chia hết cho 9
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
Đúng 0
Bình luận (0)
chứng minh rằng
ab + ba chia hết cho 11
ab - ba chia hết cho 9
( a > b )
đặt c = a+ b
ta có: ab¯ + ba¯ =cc¯
mà cc¯ chia hết cho 11 ( cc¯:11=c)
ab=10*a+b
ba=10*b+a
ab-ba=9*a-9*b=9*(a-b)=> ab-ba chia hết cho 9
Đúng 0
Bình luận (0)
ab+ba=10a + b +10b + a = 11a + 11b = 11 (a+b) chia hết cho 111
tớ chỉ giải đc 1 câu thôi còn câu b tịt
Đúng 0
Bình luận (0)
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
Đúng 0
Bình luận (0)
a,Chứng tỏ rằng ab(a+b) chia hết cho 2 (a;b thuộc N)
b,Chứng minh rằng ab + ba chia hết cho 11
c,Chưnhs minh aaa luôn chia hết cho 37
d, Chứng minh aaabbb luôn chia hết cho 7
b) ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
Đúng 1
Bình luận (0)
Chứng minh rằng ab + ba chia hết cho 11.
Theo đề bài ra, ta có :
`ab` `+` `ba` `=` `10a` `+` `b` `+` `10b` `+ a`
`=` `11a` `+` `11b`
`=` `11` `(a+b)`
\(\rightarrow\) `11` `(a+b)` chia hết cho `11`
\(\Rightarrow\) `ab` `+` `ba` chia hết cho `11`
@Nae
Đúng 1
Bình luận (0)
Chứng minh ; a/ ab+ba chia hết cho 11 ; b/ ab-ba chia hết cho 9 với a>b ; c/ abcd - (a+b+c+d ) chia hết cho 9
a/ ab+ba chia hết cho 11
Vì tổng các số chẵn -tổng các số lẻ:(b+a)-(a+b)=0 chia hết cho 11
=>Tổng ab+ba chia hết cho 11
Đúng 0
Bình luận (0)
3. Chứng minh rằng
a)
ab ba + chia hết cho 11; b)
ab ba − chia hết cho 9 với a > b
1) Chứng minh rằng:
a, ab+ba chia hết cho 11
b, ab-ba chia hết cho 9, a > b
a,ab = 10a + b
ba = 10b + a
=>ab + ba = 11(a+b) chia het cho 11.
b,ab=10*a+b
ba=10*b+a
ab-ba=9*a-9*b=9*(a-b)=> ab-ba chia hết cho 9
Đúng 0
Bình luận (0)
a) Xét tổng ab + ba = (10 x a + b) + (10 x b + a)
= 11 x a + 11 x b
= (a +b) x 11 chia hết cho 11
b) Xét hiệu ab - ba = (10a + b) - (10b + a)
= 9 x a - 9 x b
= (a - b) x 9 chia hết cho 9
Đúng 0
Bình luận (0)
A) ab + ba = (10a + b) + ( 10b + a ) = 11a + 11b = 11(a+b)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời