giải giúp mk vs:
cho tam giác ABC cân tại A ,AD ,BE lần lượt là hai dường cao,chứng minh rằng:
b)\(\frac{1}{BE^2}=\frac{1}{BC^2}+\frac{1}{4AD^2}\)
a)\(^{BC^2=2CE\cdot AC}\)
Tam giác ABC cân tại A có 2 đường cao AD,BE ( D thuộc BC , E thuộc AC ).
Chứng minh \(\frac{1}{BC^2}+\frac{1}{4AD^2}=\frac{1}{BE}\)
Cho tam giác ABC cân tại A có đường cao AD và BE.
a/ Chứng minh \(\frac{1}{BE^2}=\frac{1}{BC^2}+\frac{1}{4AD^2}\)
b/ Chứng minh \(BC^2=2CE.CA\)
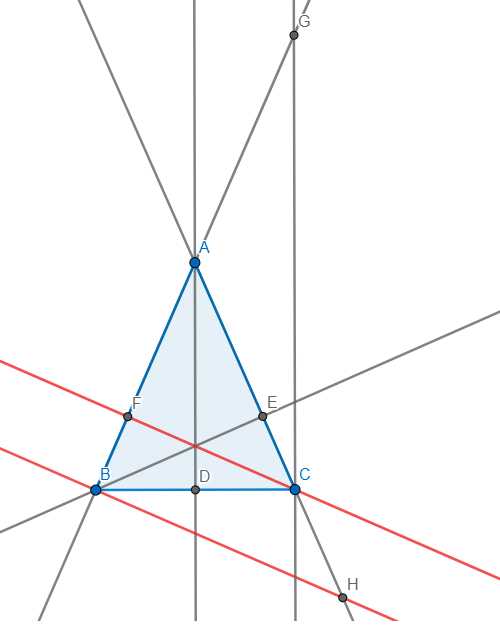
Giải giúp mình bài này với: Cho tam giác ABC cân tại A. 3 đường cao AD, BE, CF. Đường thẳng qua B và song song với CF cắt đường thẳng AC tại H. Chứng minh rằng: 1/CF*2 = 1/BC*2 + 1/4AD*2
Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)
Giúp mình !!!!!!!!
1. Tam giác ABC với D,E,F lần lượt thuộc cạnh BC,CA,AB sao cho AD,BE,CF đồng quy tại M. chứng minh \(\frac{DM}{AD}+\frac{FM}{CF}+\frac{EM}{BE}=1\)
2. Tam giác ABC với M tùy ý nằm trong tam giác. Đường thẳng đi qua M và trọng tâm G của tam giác cắt BC,CA,AB lần lượt tại A',B',C'. chứng minh: \(\frac{MA'}{GA'}+\frac{MB'}{GB'}+\frac{MC'}{GC'}=3\)
3. Tam giác nhọn ABC, phân giác AD. M,N lần lượt là hình chiếu của D trên AC,AB, P là giao điểm BM, CN. chứng minh AP vuông góc BC
Giải giúp mình bài này với:
Cho tam giác ABC cân tại A. 3 đường cao AD, BE, CF. Đường thẳng qua B và song song với CF cắt đường thẳng AC tại H. Chứng minh rằng:
1/CF*2 = 1/BC*2 + 1/4AD*2
Cho tam giác ABC cân ở A, 3 đường cao AD, BE, CF. Đường thẳng qua B song song với CF cắt AC tại H. Chứng minh
a, AC2=AE.AH
b, \(\frac{1}{CF^2}=\frac{1}{BC^2}+\frac{4}{AD^2}\)
Cô hướng dẫn nhé.
a) Do ABC là tam giác cân nên AE = AF, AC = AB
Lại có \(\Delta AFC\sim\Delta ABH\left(g-g\right)\Rightarrow\frac{AF}{AB}=\frac{AC}{AH}\Rightarrow AF.AH=AB.AC\Rightarrow AE.AH=AC^2\)
b) Câu này đề ko đúng. Cô sửa lại \(\frac{1}{CF^2}=\frac{1}{BC^2}+\frac{1}{4.AD^2}\)
\(AD.BC=AB.CF\left(=\frac{S_{ABC}}{2}\right)\)
Vậy nên \(VP=\frac{AD^2+\frac{BC^2}{4}}{BC^2.AD^2}=\frac{AD^2+\left(\frac{BC}{2}\right)^2}{CF^2AB^2}=\frac{AD^2+BD^2}{CF^2AB^2}=\frac{AB^2}{CF^2.AB^2}=\frac{1}{CF^2}=VT\)
Cho tam giác ABC cân tại A. 3 đường cao AD, BE và CF. Đường thẳng qua B và song song với CF cắt đường thẳng AC tại H. Chứng minh rằng:
1/CF^2 = 1/BC^2 + 1/4AD^2
Giải giúp mình với. Cảm ơn nhiều :D
Cho tam giác ABC cân tại A có AB=AC=50 cm; BC=60 cm. Các đường cao AD và CE cắt nhau tại H.
a) Tính CH?
b) C/m: \(\frac{1}{CE^2}=\frac{1}{BC^2}+\frac{1}{4AD^2}\)
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H \(\left(D\in BC,E\in AC,F\in AB\right).\) Gôi I là trung điểm của BC và K là đỉnh thứ tư của hình bình hành BHCK.
1) Chứng minh điểm K nằm trên đường tròn (O) và AH = 2.OI
2) Các tia AD, BE, CF lần lượt cắt đường tròn (O) tại A', B', C'. Chứng minh \(\frac{AA'}{AD}+\frac{BB'}{BE}+\frac{CC'}{CF}=4\)
3) Gọi M là giao điểm của AH và EF, N là giao điểm của AK và BC. Chứng minh MN // HK.
Giúp mk nhé m.n, ai nhanh nhất mk tick!!!
a) Do BHCK là hình bình hành nên BH // KC \(\Rightarrow KC\perp AC\Rightarrow\widehat{ACK}=90^o\)
KB // CF \(\Rightarrow\widehat{ABK}=90^o\)
Hai tam giác vuông ABK và ACK chung cạnh huyền AK nên A, B, C, K cùng thuộc đường tròn đường kính AK. Vậy K thuộc đường tròn (O).
b) Do BHCK là hình bình hành nên I là trung điểm HK.
AK là đường kính nên \(\widehat{AA'K}=90^o\Rightarrow\) DI // A'K
Vậy DI là đường trung bình tam giác HA'K. Suy ra HD = DA'
Tương tự : HF = FC' ; HE = EB'
Ta có : \(\frac{AA'}{AD}+\frac{BB'}{BE}+\frac{CC'}{CF}=\frac{AD+DA'}{AD}+\frac{BE+EE'}{BE}+\frac{CF+FC'}{CF}\)
\(=1+\frac{DA'}{AD}+1+\frac{EB'}{BE}+1+\frac{FC'}{CF}=3+\left(\frac{DA'}{AD}+\frac{EB'}{BE}+\frac{FC'}{CF}\right)\)
\(=3+\left(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\right)=3+\left(\frac{S_{BHC}}{S_{ABC}}+\frac{S_{AHC}}{S_{ABC}}+\frac{S_{AHB}}{S_{ABC}}\right)\)
\(=3+\frac{S_{ABC}}{S_{ABC}}=3+1=4\)
Vậy nên \(\frac{AA'}{AD}+\frac{BB'}{BE}+\frac{CC'}{CF}=4\)
c) Ta thấy \(\widehat{AKC}=\widehat{ABC}=\widehat{AHF}\)
Vậy nên \(\Delta AFH\sim\Delta ACK\left(g-g\right)\Rightarrow\frac{AH}{AK}=\frac{AF}{AC}\) (1)
AFH và AEH là các tam giác vuông chung cạnh huyền AH nên AFHE là tứ giác nội tiếp.
Vậy thì \(\widehat{AFM}=\widehat{AHE}=\widehat{ACN}\)
Lại có \(\Delta AFH\sim\Delta ACK\Rightarrow\widehat{FAM}=\widehat{CAN}\)
Nên \(\Delta AFM\sim\Delta ACN\left(g-g\right)\Rightarrow\frac{AF}{AC}=\frac{AM}{AN}\) (2)
Từ (1) và (2) suy ra \(\frac{AH}{AK}=\frac{AM}{AN}\Rightarrow\frac{AH}{AM}=\frac{AK}{AN}\Rightarrow\) MN // HK (Định lý Talet đảo)
em phục cô luôn rồi!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
cô giỏi thật