Ta có

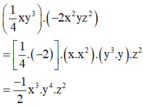
Đơn thức trên có hệ số bằng -1/2.

Bậc của tích trên là tổng bậc của các biến :

Biến x có bậc 3

Biến y có bậc 4

Biến z có bậc 2

⇒ Tích có bậc : 3 + 4 + 2 = 9.

(-2x2yz).(-3xy3z) = [(-2).(-3)].(x2.x)(y.y3).(z.z) = 6.x3.y4.z2

Đơn thức trên có hệ số bằng 6.

Bậc của tích trên là tổng bậc của các biến :

Biến x có bậc 3

Biến y có bậc 4

Biến z có bậc 2

⇒ Tích có bậc : 3 + 4 + 2 = 9

-12x³4y³3z³

^{đa thức có Bậc 3}

1. 

Tại x = -1, có : 

2.(-1)² - 5.(-1) + 2 

= 2.1 + 5 + 2 

= 9 

Tại x = \(\dfrac{1}{2}\), có : 

\(2.\left(\dfrac{1}{2}\right)^2-5.\dfrac{1}{2}+2\)

= \(2.\dfrac{1}{4}-2,5+2\)

= 0,5 - 2,5 + 2

= 0

2. 

\(\dfrac{1}{2}xy^2.\left(-3xyz\right).2x^2z\)

= -3x⁴y³z²

- Hệ số : -3

- Bậc : 9

thay x =-1 vào bt ta được

\(2\left(-1\right)^2-5\left(-1\right)+2=2+5+2=9\)

thay x=1/2 vào bt ta được 

\(2.\left(\dfrac{1}{2}\right)^2-5.\dfrac{1}{2}+2=\dfrac{1}{2}-\dfrac{5}{2}+\dfrac{4}{2}=0\)

\(\dfrac{1}{2}xy^2.-3xyz.2x^2z=-3x^4y^3z\)²

hệ số là -3 bậc 9

Tích của đơn thức : -1/2x^3y^4z^2
Bậc : 4
hệ số: -1/2

a) \(5x^2y^3z\cdot\left(-11xyz^4\right)=\left(-11\cdot5\right)\cdot\left(x^2\cdot x\right)\cdot\left(y^3\cdot y\right)\cdot\left(z\cdot z^4\right)=-55x^3y^4z^5\)

Phần biến: \(x^3y^4z^5\)

Hệ số: -55

Bậc của đơn thức: 12

b) \(-6x^4y^4\cdot\left(\dfrac{-2}{3}x^5y^3z^2\right)=\left(-6\cdot\dfrac{-2}{3}\right)\cdot\left(x^4\cdot x^5\right)\cdot\left(y^4\cdot y^3\right)\cdot z^2=4x^9y^7z^2\)

Phần biến: \(x^9y^7z^2\)

Hệ số: 4

Bậc của đơn thức: 18

a) 

Phần biến: 

Hệ số: -55

Bậc của đơn thức: 12

b) 

a) 

Phần biến: 

Hệ số: -55

Bậc của đơn thức: 12

b) 

\(\left(-\dfrac{1}{4}x^2y^3\right)\left(\dfrac{6}{5}xy^2\right)\\ =\left(-\dfrac{1}{4}.\dfrac{6}{5}\right)\left(x^2.x\right)\left(y^3.y^2\right)\\ =-\dfrac{3}{10}x^3y^5\)

Hệ số: \(-\dfrac{3}{10}\)

Biến:x³y⁵

Bậc:8

Ta có: \(3x^2\cdot\left(\dfrac{1}{6}\right)^2\cdot y^2\)

\(=3\cdot\dfrac{1}{36}\cdot x^2\cdot y^2\)

\(=\dfrac{1}{12}x^2y^2\)

Hệ số là \(\dfrac{1}{12}\)

Phần biến là \(x^2;y^2\)

Bậc là 4