Cho tam giác ABC, góc B lớn hơn góc C, đường cao AH, phân giác AM của góc BAC. Chứng minh rằng:
\(\widehat{MAH}\)= \(\frac{\widehat{B}-\widehat{C}}{2}\)
Những câu hỏi liên quan
Cho tam giác ABC có góc widehat{B}widehat{C} . Kẻ AH vuông góc với BC. Kẻ tia phân giác AD của góc widehat{BAC} (D inBC) a) Chứng minh rằng widehat{HAD}frac{widehat{B}-widehat{C}}{2} b) Tính widehat{A}, biết widehat{HAD15} và 3widehat{B}5widehat{C}
Đọc tiếp
Cho tam giác ABC có góc \(\widehat{B}>\widehat{C}\) . Kẻ AH vuông góc với BC. Kẻ tia phân giác AD của góc \(\widehat{BAC}\) (D \(\in\)BC)
a) Chứng minh rằng \(\widehat{HAD}=\frac{\widehat{B}-\widehat{C}}{2}\)
b) Tính \(\widehat{A}\), biết \(\widehat{HAD=15}\) và \(3\widehat{B}=5\widehat{C}\)
cho tam giác ABC có \(\widehat{B}>\widehat{C}\) . Kẻ đường cao AH và đường phân giác AD .
a) Chứng minh rằng \(\widehat{HAD}=\frac{\widehat{B}-\widehat{C}}{2}\)
b) Tính góc A biết : \(\widehat{HAD}=15^0\) và \(\widehat{3B}=\widehat{5C}\) .
em gửi bài qua fb thầy HD cho, tìm fb của thầy bằng sđt: 0975705122, ở đây thầy không vẽ hình được
Đúng 0
Bình luận (0)
9 tháng 10 2023 lúc 19:09
Cho tam giác ABC có \(\widehat{B}\) = 90◦ và \(\widehat{A}=\widehat{C}\) . Hai tia phân giác AD và CE lần lượt của các góc \(\widehat{BAC},\widehat{ACB}\) cắt nhau tại I. Chứng minh rằng ID = IE.
nhanh lên mình cần gấp lắm
giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu
Đúng 0
Bình luận (0)
Cho tam giác ABC , O là điểm nằm trong tam giác.
a. Chứng minh rằng : \(\widehat{BOC}\)= \(\widehat{A}+\widehat{ABO}+\widehat{ACO}\)
b. Biết \(\widehat{ABO}+\widehat{ACO}=90-\frac{\widehat{A}}{2}\)và tia BO là tia phân giác của góc B. Chứng minh rằng : Tia CO là tia phân giác của góc C.
a) Ta có: + \(\widehat{BOC}\)là góc ngoài của tam giác OBK
=> \(\widehat{BOC}=\widehat{OBK}+\widehat{OKB}\) (1)
+ \(\widehat{OKB}\)là góc ngoài của tam giác AKC
=>\(\widehat{OKB}=\widehat{A}+\widehat{ACK}\)(2)
Từ (1)(2) =>\(\widehat{BOC}=\widehat{OBK}+\widehat{A}+\widehat{ACK}\)
hay\(\widehat{BOC}=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)
b) Ta có:\(\widehat{ABO}+\widehat{ACO}=90^o-\frac{\widehat{A}}{2}\)
=>\(2\widehat{ABO}+2\widehat{ACO}=180^o-\widehat{A}\)(3)
Xét tam giác ABC có:
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)( Tổng 3 góc trong 1 tam giác)
=>\(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{A}\)(4)
Từ (3)(4) => \(2\widehat{ABO}+2\widehat{ACO}=\widehat{ABC}+\widehat{ACB}\)(*)
Ta có: BO là tia phân giác của góc ACB
=>\(2\widehat{ABO}=\widehat{ABC}\)(**)
Từ (*)(**) => \(2\widehat{ABO}+2\widehat{ACO}=2\widehat{ABO}+\widehat{ACB}\)
=>\(2\widehat{ACO}=\widehat{ACB}\)
=> CO là tia phân giác của góc ACB
Đúng 1
Bình luận (0)
Cho tam giác ABC (có AB lớn hơn AC) M là trung điểm của BC đường thẳng vuông góc với tia phân giác của góc A tại M cắt cạnh AB; AC lần lượt tại E và F chứng minh
a) EH=HF
B)\(2\widehat{BME}=\widehat{ACB}-\widehat{B}\)
c) \(\frac{FE^2}{4}+AH^2=AE^2\)
d) BE=CF
BIET DAP AN BAI NAY O AU KHONG
Cho tam giác ABC (có AB lớn hơn AC) M là trung điểm của BC đường thẳng vuông góc với tia phân giác của góc A tại M cắt cạnh AB; AC lần lượt tại E và F chứng minh
a) EH=HF
B\(2\widehat{BMe}=\widehat{ACB}-\widehat{B}\)
c)\(\frac{FE^2}{4}+AH^2=AE^2\)
d) BE=CF
a ) AH là phân giác của \(\widehat{BAC}\)
\(\Rightarrow\widehat{EAH}=\widehat{FAH}\)
Xét 2 tam giác vuông ΔEAH và ΔFAH có:
AH chung
\(\widehat{EAH}=\widehat{FAH}\)
=> ΔEAH = ΔFAH (cạnh góc vuông - góc nhọn)
=> EH = FH (đpcm)
b ) \(\widehat{ACB}\) là góc ngoài tại C của ΔMCF
\(\Rightarrow\widehat{ACB}=\widehat{CFM}+\widehat{CMF}\)
\(\widehat{AEF}\) là góc ngoài tại E của ΔMBE
\(\Rightarrow\widehat{AEF}=\widehat{EMB}+\widehat{ABC}\)
Lại có : \(\widehat{CFM}=\widehat{AEF}\) (do ΔEAH = ΔFAH)
\(\Rightarrow\widehat{ACB}=\widehat{EMB}+\widehat{ABC}+\widehat{CMF}\)
Mặt khác \(\widehat{EMB}=\widehat{CMF}\) (đối đỉnh)
\(\Rightarrow\widehat{ACB}=2.\widehat{EMB}+\widehat{ABC}\)
Hay \(2.\widehat{BME}=\widehat{ACB}-\widehat{ABC}\)( ĐPCM )
c, ΔAHE vuông tại H
\(\Rightarrow HE^2+AH^2=AE^2\)
ΔEAH = ΔFAH ⇒ HE = HF => H là trung điểm của FE
\(\Rightarrow HE=\frac{FE}{2}\)
\(\Rightarrow HE^2=\left(\frac{FE}{2}\right)^2=\frac{FE^2}{4}\)
\(\Rightarrow\frac{FE^2}{4}+AH^2=AE^2\left(đpcm\right)\)
, Qua C kẻ đường thẳng song song với AB cắt EF ở D.
CD ║ AB \(\Rightarrow\widehat{CDF}=\widehat{AEH}\) (đồng vị)
mà \(\widehat{AFH\:}=\widehat{AEH}\)(ΔEAH = ΔFAH)
\(\Rightarrow\widehat{CDF}=\widehat{AFH\:}\)
=> ΔCDF cân tại C
=> CD = CF
Dễ dàng chứng minh được ΔMBE = ΔMCD (g.c.g)
⇒ BE = CD mà CD = CF
⇒ BE = CF (đpcm)
19 tháng 8 2021 lúc 15:34
Cho tam giác ABC, góc B > góc C. Đường thẳng chứa tia phân giác góc ngoài tại đỉnh A cắt đường thẳng BC tại N. Tia phân giác trong của góc A cắt BC tại M. Chứng minh \(\widehat{ANC}=\dfrac{\widehat{AMC}-\widehat{AMB}}2\).
cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. AH kéo dài cắt đường tròn (O;R) tại D:
a, Chứng minh rằng\(\widehat{BAH}=\widehat{CAO}\)
b, Giả sử AH=R. Chứng minh rằng: \(\widehat{BAC}=60^o\)
c, Tính tổng: \(^{AB^2+BD^2+DC^2+CA^2}\)theo R
Cho tam giác ABC có \(\widehat B > \widehat C\). Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh \(\widehat {ADB} < \widehat {ADC}\).
b) Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx} = \widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: \(\Delta ABD = \Delta AED,AB < AC\).
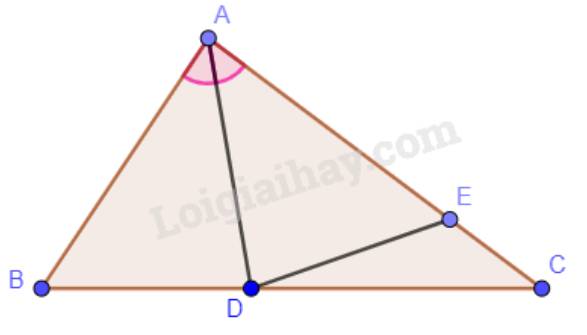
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).
Đúng 0
Bình luận (0)