Giải ptrinh
1x+1x+1x=11x+1+1x
Giải các phương trình sau:
a) x − 2 x + x x + 2 = 2 ;
b) 2 x + 1 − 1 x − 2 = 3 x − 11 x + 1 x − 2 ;
c) 5 + 96 x 2 − 16 = 2 x − 1 x + 4 + 3 x − 1 x − 4 ;
d) 2 x + 2 − 2 x 2 + 16 x 3 + 8 = 5 x 2 − 2 x + 4 .
Giải phương trình: 1 x - 1 + 1 x - 2 = 1 x + 2 + 1 x + 1
ĐKXĐ: x ≠ ± 1;x ≠ ± 2
Phương trình
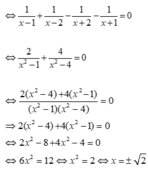
Vậy tập nghiệm của phương trình là S = { ± √ 2 }
Giải các phương trình: x + 1 x - 1 - x - 1 x + 1 1 + x + 1 x - 1 = x - 1 2 x + 1
Cách 1. ĐKXĐ: x ≠ ± 1. Biến đổi vế trái thành 4 x x 2 - 1 . x - 1 2 x = 2 x + 1
Ta đưa phương trình đã cho về dạng 2 x + 1 = x - 1 2 x + 1
Giải phương trình này bằng cách khử mẫu:
4(x + 1) = (x − 1)(x + 1)
⇔(x + 1)(x − 5) = 0
⇔x = −1 hoặc x = 5
Trong hai giá trị vừa tìm được, chỉ có x = 5 là thỏa mãn ĐKXĐ.
Vậy phương trình đã cho có một nghiệm duy nhất x = 5.
Cách 2. Đặt x + 1 x - 1 = y ta có phương trình y - 1 y 1 + y = 1 2 y
ĐKXĐ của phương trình này là y ≠ 0 và y ≠ −1. Giải phương trình này bằng cách khử mẫu:
2 y 2 − 2 = 1 + y
⇔2( y 2 − 1)−(y + 1) = 0
⇔(y + 1)(2y − 3) = 0
⇔y = −1 hoặc y = 3/2
Trong hai giá trị tìm được, chỉ có y = 3/2 là thỏa mãn ĐKXĐ
Vậy phương trình đã cho tương đương với phương trình x + 1 x - 1 = 3 2
Giải phương trình này ta được x = 5
Giải các phương trình sau: 1 - x - 1 x + 1 ( x + 2 ) = x + 1 x - 1 + x - 1 x + 1
ĐKXĐ: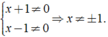
Ta có: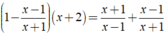
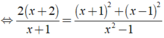
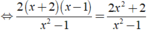
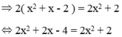
⇔ 2x = 6 ⇔ x = 3.
Vậy phương trình đã cho có nghiệm là x = 3.
Giải các phương trình sau: 1 - x - 1 x + 1 ( x + 2 ) = x + 1 x - 1 + x - 1 x + 1
ĐKXĐ: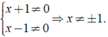
Ta có: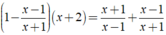
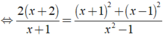
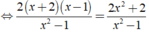
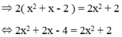
⇔ 2x = 6 ⇔ x = 3.
Vậy phương trình đã cho có nghiệm là x = 3.
Giải các phương trình sau 1 - 2 x - 1 x + 1 3 + 6 1 - 2 x - 1 x + 1 2 = 12 2 x - 1 x + 1 - 20
Đặt y = 1 - 2 x - 1 x + 1 , ta có:
12 2 x - 1 x + 1 - 20 = - 12 1 - 2 x - 1 x + 1 - 8 = - 12 y - 8
Do đó phương trình đã cho có dạng y 3 + 6 y 2 = −12y − 8
Giải phương trình này:
y 3 + 6 y 2 = −12y − 8
⇔ y 3 + 3 y 2 .2 + 3y. 2 2 + 2 3 = 0
⇔ y + 3 3 = 0
⇔y =−2
Vậy phương trình đã cho tương đương với phương trình
1 - 2 x - 1 x + 1 = - 2 h a y 2 x - 1 x + 1 = 3
ĐKXĐ của phương trình là x ≠ -1. Giải phương trình này bằng cách khử mẫu, ta được:
2x − 1 = 3(x + 1)
⇔x = −4
Giá trị x = -4 thỏa mãn ĐKXĐ nên là nghiệm của phương trình đã cho.
Chứng minh:
1 x x + 1 + 1 x + 1 x + 2 + 1 x + 2 x + 3 + 1 x + 3 x + 4 + 1 x + 4 x + 5 + 1 x + 5
Giải phương trình: 2 x - 1 x - 1 + 1 = 1 x - 1
Điều kiện xác định: x ≠ 1.
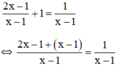
Suy ra: 2x – 1 + x – 1 = 1
⇔ 3x – 2 = 1
⇔ 3x = 3
⇔ x = 1 (không thỏa mãn điều kiện xác định).
Vậy phương trình vô nghiệm.
Giải phương trình: 1 x + 2 = 1 x + 2 x 2 + 1
Giải bất phương trình: 1 x + 1 < 1 x - 1 2
Điều kiện xác định x ≠ 1 và x ≠ –1.
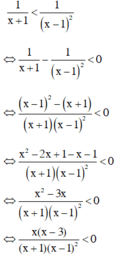
Đặt 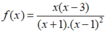 . Ta có bảng xét dấu sau:
. Ta có bảng xét dấu sau:
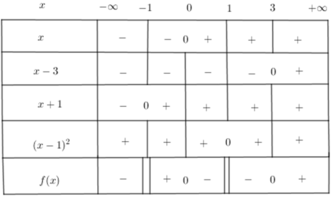
Dựa vào bảng xét dấu ta thấy
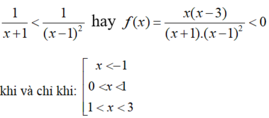
Vậy bất phương trình có tập nghiệm S = (–∞; –1) ∪ (0; 1) ∪ (1; 3)