tìm x
x : 13 = 41
8 . ( x - 3 ) = 0
Những câu hỏi liên quan
Tìm x
a) 14x - 9x + 54 = 132
b) 218 + 2.( x - 45) = (-12) + 418
c) |x-3| : 32 = 30
a) 14x - 9x + 54 = 132
5x + 54 = 169
5x = 169 - 54
5x = 115
x = 115 : 5
x = 23
b) 218 + 2( x - 45 ) = (-12) + 418
218 + 2( x - 45 ) = +( 418 - 12 )
218 + 2( x - 45 ) = 406
2( x - 45 ) = 406 - 218
2( x - 45 ) = 188
x - 45 = 188 : 2
x - 45 = 94
x = 94 + 45
x = 139
c)\(|x-3|\) : 32 = 30
( x - 3 ) : 9 = 1
=> x - 3 = 1 . 9
x - 3 = 9
x = 9 + 3
x = 12
Đúng 0
Bình luận (0)
a) 14x - 9x + 54 = 132
=> ( 14 - 9 ) . x + 54 = 169
=> 5x + 54 = 169
=> 5x = 115
=> x = 23
b) 218 + 2( x - 45 ) = ( - 12 ) + 418
=> 218 + 2( x - 45 ) = 406
=> 2( x - 45 ) = 188
=> x - 45 = 94
=> x = 139
c) \(|x-3|:3^2=3^0\)
\(\Rightarrow|x-3|=9\)
\(\Rightarrow|x-3|=-9\)
\(\Rightarrow\orbr{\begin{cases}x-3=9\\x-3=-9\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=12\\x=-6\end{cases}}\)
Đúng 0
Bình luận (0)
Biến đổi các biểu thức sau thành phân thức:a)
M
4
−
4
n
m
+
n
2
m
2
1
m
−
2...
Đọc tiếp
Biến đổi các biểu thức sau thành phân thức:
a) M = 4 − 4 n m + n 2 m 2 1 m − 2 n với m ≠ 0 , n ≠ 0 , n ≠ 2 m ;
b) N = 1 3 + x 1 − x x + 3 với x≠−3.
a) Ta có M = ( 2 m − n ) 2 m 2 . mn n − 2 m = ( n − 2 m ) n m
b) Ta có N = 1 3 + x ( x + 3 ) 3 = x 2 + 3 x + 1 3
Đúng 0
Bình luận (0)
Tìm x, biết:a) (x - 32) - 68 0; b) 274 - ( 9.x + 18) 4c) 442 + (418 - x) 860;d) 107 + (210 - x) 317
Đọc tiếp
Tìm x, biết:
a) (x - 32) - 68 = 0;
b) 274 - ( 9.x + 18) = 4
c) 442 + (418 - x) = 860;
d) 107 + (210 - x) = 317
a) x = 100.
b) x = 28.
c) x = 0.
d) x = 0.
Đúng 0
Bình luận (0)
Bài cô t vừa giao nè
tìm x
x^3 - x^2 - 4 = 0
Lời giải:
PT $\Leftrightarrow (x^3-2x^2)+(x^2-4)=0$
$\Leftrightarrow x^2(x-2)+(x-2)(x+2)=0$
$\Leftrightarrow (x-2)(x^2+x+2)=0$
$\Rightarrow x-2=0$ hoặc $x^2+x+2=0$
Nếu $x-2=0\Leftrightarrow x=2$ (tm)
Nếu $x^2+x+2=0$
$\Leftrightarrow (x+\frac{1}{2})^2=-\frac{7}{4}<0$ (vô lý)
Vậy pt có nghiệm duy nhất $x=2$
Đúng 1
Bình luận (0)
G = (x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)(x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)
a) Rút gọn G b) Tìm giá trị nhỏ nhất của G với x > 0
c) Tính G tại | x - 3 | = 2 d) Tìm x với G = 1 ; G < 0
Tìm x, biết: 3 x - 3 - 6 x 9 - x 2 + x x + 3 = 0
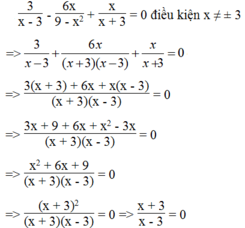
Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0
Ta có: x + 3 = 0 => x = -3 (không thỏa mãn điều kiện)
Vậy không có giá trị nào của x để biểu thức bằng 0.
Đúng 0
Bình luận (0)
Tìm chữ số x, biết
a) (80x-801) x 12 =0 b) (x1-10) x 32 = 32
c) x x x = 16 d) (xx + xx) x 0 = 0
a. (80x - 801) . 12 = 0
<=> 80x - 801 = 0
<=> 80x = 801
<=> x = \(\dfrac{801}{80}\)
(Mấy câu tiếp mik ko hiểu đề, bn viết lại để dễ hiểu hơn nhé)
Đúng 1
Bình luận (0)
c: Ta có: \(\overline{xxx}=16\)
\(\Leftrightarrow100x+10x+1=16\)
\(\Leftrightarrow101x=16\)
hay \(x=\dfrac{16}{101}\)
Đúng 0
Bình luận (0)
tìm x
x^3 -2x^2+x-2=0
2x(3x-5)=10-6x
4-x=2(x-4)^2
4-6x+x(3x-2)=0
\(x^3-2x^2+x-2=0\\ \Leftrightarrow x^2\left(x-2\right)+\left(x-2\right)=0\\ \Leftrightarrow\left(x^2+1\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=2\end{matrix}\right.\\ Vậy:x=2\\ ---\\ 2x\left(3x-5\right)=10-6x\\ \Leftrightarrow6x^2-10x-10+6x=0\\ \Leftrightarrow6x^2-4x-10=0\\ \Leftrightarrow6x^2+6x-10x-10=0\\ \Leftrightarrow6x\left(x+1\right)-10\left(x+1\right)=0\\ \Leftrightarrow\left(6x-10\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}6x-10=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-1\end{matrix}\right.\)
Đúng 1
Bình luận (1)
\(4-x=2\left(x-4\right)^2\\ \Leftrightarrow4-x=2\left(x^2-8x+16\right)\\ \Leftrightarrow2x^2-16x+32+x-4=0\\ \Leftrightarrow2x^2-15x+28=0\\ \Leftrightarrow2x^2-8x-7x+28=0\\ \Leftrightarrow2x\left(x-4\right)-7\left(x-4\right)=0\\ \Leftrightarrow\left(2x-7\right)\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-7=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=4\end{matrix}\right.\\ ---\\ 4-6x+x\left(3x-2\right)=0\\ \Leftrightarrow4-6x+3x^2-2x=0\\ \Leftrightarrow3x^2-8x+4=0\\ \Leftrightarrow3x^2-6x-2x+4=0\\ \Leftrightarrow3x\left(x-2\right)-2\left(x-2\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho hàm số
f
(
x
)
3
-
9
-
x
x
,
0
x
9...
Đọc tiếp
Cho hàm số f ( x ) = 3 - 9 - x x , 0 < x < 9 m , x = 0 3 x , x ≥ 9 . Tìm m để f(x) liên tục trên [ 0 ; + ∞ )
A. 1 3
B. 1 2
C. 1 6
D. 1
Cho hàm số
f
(
x
)
3
-
9
-
x
x
,
0
x...
Đọc tiếp
Cho hàm số f ( x ) = 3 - 9 - x x , 0 < x < 9 m , x = 0 3 x , x ≥ 9 Tìm m để f(x) liên tục trên [0; +∞) là.
A. 1/3.
B. 1/2.
C. 1/6.
D. 1.
Chọn C.
TXĐ: D = [0; +∞).
Với x = 0 ta có f(0) = m.
Ta có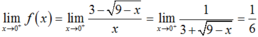 
.
Vậy để hàm số liên tục trên [0; +∞) khi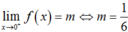 
.
Đúng 0
Bình luận (0)