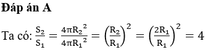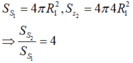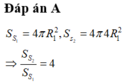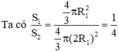Cho mặt cầu (S1) bán kính R1, mặt cầu (S2) bán kính R2 = 2R1 . Tìm tỉ số diện tích của mặt cầu (S2) và (S1).

Những câu hỏi liên quan
Cho mặt cầu
S
1
có bán kính
R
1
,
mặt cầu
S
2
có bán kính
R
2
2
R
1
.
Tính tỉ số diện tích của mặt cầu
S
2
và ...
Đọc tiếp
Cho mặt cầu S 1 có bán kính R 1 , mặt cầu S 2 có bán kính R 2 = 2 R 1 . Tính tỉ số diện tích của mặt cầu S 2 và S 1 ?
A. 4
B. 3
C. 1/2
D. 2
Đáp án A
S S 1 = 4 π R 1 2 , S s 2 = 4 π 4 R 1 2 ⇒ S S 2 S S 1 = 4
Đúng 0
Bình luận (0)
Cho mặt cầu
(
S
1
)
có bán kính
R
1
, cho mặt cầu
(
S
2
)
có bán kính
R
2
2
R
1
. Tính tỉ số diện tích của mặt cầu
(
S
2
)
và
(
S
1...
Đọc tiếp
Cho mặt cầu ( S 1 ) có bán kính R 1 , cho mặt cầu ( S 2 ) có bán kính R 2 = 2 R 1 . Tính tỉ số diện tích của mặt cầu ( S 2 ) và ( S 1 )
A. 1 2
B. 3
C. 4
D. 2
Cho mặt cầu
(
S
1
)
có bán kính
R
1
, mặt cầu
(
S
2
)
có bán kính
R
2
2
R
1
. Tính tỷ số diện tích của mặt cầu
(
S
1
)
v
à
(
S
2...
Đọc tiếp
Cho mặt cầu ( S 1 ) có bán kính R 1 , mặt cầu ( S 2 ) có bán kính R 2 = 2 R 1 . Tính tỷ số diện tích của mặt cầu ( S 1 ) v à ( S 2 ) ?
A. 4
B. 3
C. 1 2
D. 2
Cho mặt cầu
(
S
1
)
có bán kính
R
1
, mặt cầu
S
2
có bán kính
R
2
2
R
1
. Tính tỷ số diện tích của mặt cầu
(
S
1
)
và
(
S
2
)
? A. 4...
Đọc tiếp
Cho mặt cầu ( S 1 ) có bán kính R 1 , mặt cầu S 2 có bán kính R 2 = 2 R 1 . Tính tỷ số diện tích của mặt cầu ( S 1 ) và ( S 2 ) ?
A. 4
B. 3
C. 1 2
D. 2
Cho mặt cầu (
S
1
) có bán kính
R
1
, mặt cầu (
S
2
) có bán kính
R
2
2
R
1
. Tính tỉ số diện tích của mặt cầu
(
S
1
)
và
(
S
2
)...
Đọc tiếp
Cho mặt cầu ( S 1 ) có bán kính R 1 , mặt cầu ( S 2 ) có bán kính R 2 = 2 R 1 . Tính tỉ số diện tích của mặt cầu ( S 1 ) và ( S 2 ) ?
A. 4.
B. 3.
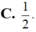
D. 2.
Cho mặt cầu
S
1
có bán kính
R
1
, mặt cầu
S
2
có bán kính Tính tỉ số diện tích của mặt cầu
S
1
và
S
2
? A. 4 B. 3 C.
1
2
D. 2
Đọc tiếp
Cho mặt cầu S 1 có bán kính R 1 , mặt cầu S 2 có bán kính Tính tỉ số diện tích của mặt cầu S 1 và S 2 ?
A. 4
B. 3
C. 1 2
D. 2
Gọi
S
1
là diện tích mặt cầu tâm
O
1
có bán kính
R
1
,
S
2
là diện tích mặt cầu tâm
O
2
có bán kính
R
2
2
R...
Đọc tiếp
Gọi S 1 là diện tích mặt cầu tâm O 1 có bán kính R 1 , S 2 là diện tích mặt cầu tâm O 2 có bán kính R 2 = 2 R 1 . Tính tỷ số S 1 S 2
A. 2
B. 4
C. 1 2
D. 1 4
Cho tứ diện đều ABCD có mặt cầu nội tiếp là
S
1
và mặt cầu ngoại tiếp là
S
2
. Một hình lập phương ngoại tiếp
S
2
và nội tiếp trong mặt cầu
S
2
. Gọi
r
1
,
r
2
,
...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu S 1 , S 2 , S 3 . Khẳng định nào sau đây đúng?
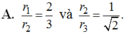
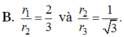
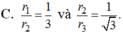
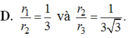
Cho tứ diện đều ABCD có mặt cầu nội tiếp là
S
1
và mặt cầu ngoại tiếp là
S
2
. Một hình lập phương ngoại tiếp
S
2
và nội tiếp trong mặt cầu
S
2
. Gọi
r
1
,
r
2...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu ( S 1 ) , ( S 2 ) , ( S 3 ) . Khẳng định nào sau đây đúng?
A. r 1 r 2 = 2 3 và r 2 r 3 = 1 2 .
B. r 1 r 2 = 2 3 và r 2 r 3 = 1 3 .
C. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 .
D. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 3 .