mn cho e hỏi cách giải chi tiết câu này với ạ:
Chứng minh rằng tam giác ABC vuông nếu sin^2A+sin^B+sin^2C=2
em cảm ơn ạ
Những câu hỏi liên quan
22 tháng 7 2023 lúc 22:21
Cho tam giác abc vuông ở a chứng tỏ sin b < cot c
xin cảm ơn mọi người nhiều nhiều ạ
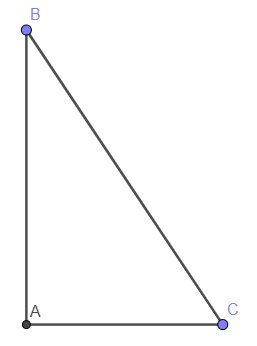
Xét \(\Delta ABC\) vuông tại A có:
\(sin\left(B\right)=\dfrac{AC}{BC}\)
\(cotg\left(C\right)=\dfrac{AC}{AB}\)
BC là cạnh huyền của \(\Delta ABC\) \(\left(AB,AC< BC\right)\)
\(\Rightarrow\dfrac{AC}{BC}< \dfrac{AC}{AB}\Rightarrow sin\left(B\right)< cotg\left(C\right)\)
Đúng 2
Bình luận (0)
cho tam giác ABC thỏa mãn \(\sin^2A+\sin^2B=\sqrt{\sin C}\) và A, B là hai góc nhọn. chứng minh tam giác ABC vuông tại C
cho tam giác abc vuong tại A trên cạnh AB lấy điểm M Vẽ MN vuông góc với BC chứng minh sin C=AN/CM?
Giup em với ạ
Ta có A và N cùng nhìn MC dưới góc 90 độ
=> AMNC là tứ giác nội tiếp
\(\Rightarrow\widehat{BAN}=\widehat{BCM}\) (góc nội tiếp cùng chắn cungMN)
Xét tg ABN và tg CBM có
\(\widehat{BAN}=\widehat{BCM}\) (cmt)
\(\widehat{ABC}\) chung
=> tg ABN đồng dạng tg CBM (g.g.g)
\(\Rightarrow\dfrac{AN}{CM}=\dfrac{AB}{BC}\)
Xét tg vuông ABC
\(\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\Rightarrow\sin\widehat{C}=\dfrac{AN}{CM}\) (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn, 3 đường cao BD,CE,AF cắt nhau tại H. Chứng minh:2<sin^2A+sin^2B+sin^2C<3
cho tam giác ABC thỏa mãn \(\sin^2A+\sin^2B=\sqrt{\sin C}\) và A, B là hai góc nhọn. chứng minh tam giác ABC vuông tại C
Cho tam giác ABC biết AB12cm , AC9cm , BC15cm. a. Chứng minh tam giác ABC vuôngb. Tính; frac{sin B+sin C}{sin B-sin C} c. Tính độ dài đường cao AHd. Gọi M và N lần lượt là hình chiếu của H trên AB và AC. Chứng minh AMcdot ABANcdot AC e. Chứng minh AHfrac{BC}{cot B+cot C} f. Chứng minh S_{AMN}sin^2Bcdotsin^2Ccdot S_{ABC} Giúp mk nhanh nhé mn ơi
Đọc tiếp
Cho tam giác ABC biết AB=12cm , AC=9cm , BC=15cm.
a. Chứng minh tam giác ABC vuông
b. Tính; \(\frac{\sin B+\sin C}{\sin B-\sin C}\)
c. Tính độ dài đường cao AH
d. Gọi M và N lần lượt là hình chiếu của H trên AB và AC. Chứng minh \(AM\cdot AB=AN\cdot AC\)
e. Chứng minh \(AH=\frac{BC}{\cot B+\cot C}\)
f. Chứng minh \(S_{AMN}=\sin^2B\cdot\sin^2C\cdot S_{ABC}\)
Giúp mk nhanh nhé mn ơi
Chứng minh rằng với mọi tam giác nhọn ABC ta có:
\(\left(cosA+cosB+cosC\right)^2\le sin^2A+sin^2B+sin^2C\)
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC
Cho tam giác ABC và \(\sin^2A+\sin^2B=\dfrac{5}{2}\sin^2C\). Chứng minh rằng: \(sinC\le\dfrac{4}{5}\)