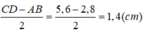Cho hình thang ABCD có đáy AB và CD. AC và BD cắt nhau tại M. Chứng
minh: AB/CD=AM/MC=BM/MD
Những câu hỏi liên quan
Cho hình thang ABCD (AB là đáy nhỏ, CD là đáy lớn). Đoạn thẳng AC và BD cắt nhau tại điểm O. Trên đoạn thẳng AB lấy điểm M sao cho AM = BM. Đường thẳng MO cắt đáy lớn CD ở điểm N. Chứng tỏ rằng NC = ND
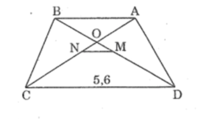
Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: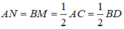 
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: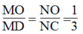 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: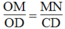 
Hệ quả định lí Ta-lét)
Suy ra: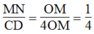 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
Đúng 0
Bình luận (0)
Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. So sánh độ dài đoạn thẳng MN với nửa hiệu của CD và AB
Cho hình thang cân ABCD đáy AB, CD có 2 đường chéo AC và BD cắt nhau tại O. Gọi M và N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 12cm. a/ Tính độ dài MN và đáy nhỏ AB. b/ So sánh độ dài MN với nửa hiệu độ dài của CD và AB.
Cho hình thang cân ABCD, AB // CD, AC < CD, MC = MD. AM cắt BD tại E, BM cắt AC tại F
a) CMR: tam giác MAD = tam giác MBC
b) tam giác MED = tam giác MFC
Cho hình thang cân ABCD có AB//CD, AB<CD, hai đường cheó AC và BD cắt nhau tại P , hai cạnh bên AD và BC kéo dài cắt nhau tại Q.C/M: PQ là đường trung trực của hai đáy hình thang cân ABCD
Xét ΔQDC có AB//DC
nên QA/AD=QB/BC
mà AD=BC
nên QA=QB
QA+AD=QD
QB+BC=QC
mà QA=QB và AD=BC
nên QD=QC
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc DBA=góc BAC
=>góc PAB=góc PBA
=>PA=PB
PA+PC=AC
PB+PD=BD
mà PA=PB và AC=BD
nên PC=PD
PA=PB
QA=QB
=>PQ là trung trực của AB
PD=PC
QD=QC
=>PQ là trung trực của DC
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AB//CD) có AB=7,5;CD=12 gọi M là trung điểm của CD, AM cắt BD tại E và BM cắt AC tại F.Chứng minh rằng
a,EF//AB
b,Tính EF
Cho hình thang ABCD (AB//CD) có AB=7,5;CD=12 gọi M là trung điểm của CD, AM cắt BD tại E và BM cắt AC tại F.Chứng minh rằng
a,EF//AB
b,Tính EF
Cho hình thang ABCD (AB//CD) có AB=7,5;CD=12 gọi M là trung điểm của CD, AM cắt BD tại E và BM cắt AC tại F.Chứng minh rằng
a,EF//AB
b,Tính EF