Link hình: file:///C:/Users/THAOCAT/Pictures/Screenshots/Screenshot%20(1224).png

Áp dụng định lý Menelaus cho bộ ba điểm (K,E,D) thằng hàng của \(\Delta\)AMC, ta được: \(\frac{KM}{KC}.\frac{EC}{EA}.\frac{DA}{DM}=1\Rightarrow\frac{KM}{KC}=\frac{EA}{EC}.\frac{DM}{DA}\)(1)

Tương tự đối với bộ ba điểm (H,D,F) thẳng hàng trong \(\Delta\)AMB, ta được: \(\frac{HB}{HM}.\frac{DM}{DA}.\frac{FA}{FB}=1\Rightarrow\frac{HB}{HM}=\frac{FB}{FA}.\frac{DA}{DM}\)(2)

Tiếp tục áp dụng định lý Ceva cho ba đường thẳng AD, BE, CF đồng quy tại M trong \(\Delta\)ABC, ta có: \(\frac{DC}{DB}.\frac{FB}{FA}.\frac{EA}{EC}=1\Rightarrow\frac{DC}{DB}=\frac{FA}{FB}.\frac{EC}{EA}\)(3)

Từ (1), (2), (3) suy ra \(\frac{KM}{KC}.\frac{HB}{HM}.\frac{DC}{DB}=1\)

\(\Delta\)BMC có \(\frac{KM}{KC}.\frac{HB}{HM}.\frac{DC}{DB}=1\)nên ba đường thẳng MD, BK, CH đồng quy (định lý Ceva đảo)

Vậy AD, BK và CH đồng quy (đpcm)

Xét bài toán (II): Cho tam giác A'B'C' điểm D' thuộc cạnh BC sao cho \(\frac{A'B'}{A'C'}=\frac{D'B'}{D'C'}\).

Chứng minh: A'D' là phân giác góc A' của tam giác A'B'C'

Trên tia đối tia D'A' lấy điểm E' sao cho B'E'=B'A' 

=> \(\Delta B'E'A'\)cân tại B'

=> \(\widehat{B'A'D'}=\widehat{B'E'D'}\)(1)

Xét tam giác: A'D'C' và tam giác E'D'B' có: \(\frac{E'B'}{A'C'}=\frac{D'B'}{D'C'}\)và \(\widehat{C'D'A'}=\widehat{B'D'E'}\)

=> Hai tam giác trên đồng dạng

=> \(\widehat{C'A'D'}=\widehat{B'E'D'}\)(2)

Từ (1), (2) => \(\widehat{C'A'D'}=\widehat{B'A'D'}\)=> A'D' là phân giác góc A của tam giác A'B'C'

Quay lại bài toán của bạn:

Xét tam giác EFD có: M thuộc FD và \(\frac{ED}{EF}=\frac{MD}{MF}\)

theo bài toán (II)  đã chứng minh ở trên ta có: EM là phân giác góc \(\widehat{FED}\)

tương tự FN là phân giác góc \(\widehat{DFE}\)

mà EM cắt FN tại H

=> H là giao ba đường phân giác trong tam giác DEF

=> DA là phân giác trong góc FDE

Như vậy cần chứng minh H là trực tâm của tam giác ABC

Bài này có thể phải dùng tới định lí Menenaus hoặc Ceva. Em đã được học về các định lý này chưa?

Bài này mình cảm thấy hơi lạ. Theo chứng minh của anh/chị Nguyễn Linh Chi thì H chính là giao điểm 3 đường phân giác của ∆DEF. Nhưng nếu F,E là 2 điểm bất kỳ nằm trên AB,AC(E,F khác chân đường cao cao kẻ từ C và B) sao cho AD là phân giác góc FDE thì H vẫn là giao điểm 3 đường phân giác của ∆DEF. Nhưng khi đó thì H không phải là trực tâm của ∆ABC. Mong mọi người "khai sáng" cái đầu của mình giùm mình huhu mình không hiểu lắm về đề bài ạ :((

Có sai sót gì xin mọi người bỏ qua ạ.

tui ko biết

ê ko bt trả lời lm chi

chán

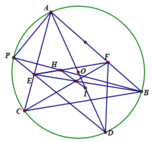
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do  H E ∥ B C ⊥ H A  ), nên tứ giác APEH nội tiếp.

Ta có A P H ^ = A E H ^  (góc nội tiếp)

= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)

⇒ P H ≡ P B

2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^  

Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF

Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF

Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF

3). Do I là tâm nội tiếp nên EI là tia phân giác trong.

Mà EA là tia phân giác ngoài, suy ra  E I ⊥ A C ⇒ E I ∥ H B

Tương tự F I ∥ H C ;   E F ∥ B C ⇒ Δ I E F   v à   Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.

a) Ta có: \(\angle BEC=\angle BFC=90\Rightarrow BCCEF\) nội tiếp

Ta có: \(\angle AFC=\angle ADC=90\Rightarrow ACDF\) nội tiếp

b) Dễ dàng chứng minh được AEHF,EHDC nội tiếp

\(\Rightarrow\angle FEH=\angle FAH=\angle FCB=\angle HED\)

\(\Rightarrow EB\) là phân giác \(\angle DEF\)

Vì \(EF\parallel XY\) \(\Rightarrow\dfrac{AX}{AY}=\dfrac{AF}{AE}\left(1\right)\)

Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle AFE=\angle ACB\end{matrix}\right.\)

\(\Rightarrow\Delta AEF\sim\Delta ABC\left(g-g\right)\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\dfrac{AX}{AY}=\dfrac{AC}{AB}\)