Gọi I là giao điểm của AH và BC

Áp dụng định lí pytago trong tam giác vuông ABI ta có

BI²=AB²-AH²

BI²=8.5²-4²=56.25

BI=căn bậc hai của 56.25

Áp dụng định lí pytago trong tam giác vuông AIC ta có

IC^2=AC^2-AI^2

HC^2=5^2-4^2=9

HI=3

Ta co BI+IC=BC

      7.5+3=10.5

Chu vi của tam giác ABC là 8.5+5+10.5=24

a) Theo đề bài ta có :

BC² = 5² = 25

AB² + AC² = 4² + 3² = 16 + 9 = 25

=> BC² = AB² + AC² ( định lý Pytago đảo )

=> Tam giác ABC vuông ( đpcm )

b) \(C_{\Delta ABC}=AB+AC+BC=3+4+5=12cm\)

a: \(AC=\sqrt{AB^2+BC^2}=2\sqrt{13}\left(cm\right)\)

\(C=AB+BC+AC=10+2\sqrt{13}\left(cm\right)\)

Áp dụng định lí Py - ta - go vào tam giác vuông ABC ta có:

\(AC=\sqrt{4^2+6^2}=\sqrt{52}=2\sqrt{13}\)

Chu vi tam giác ABC là:

\(4+6+2\sqrt{13}=10+2\sqrt{13}\)

Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:

\(AC^2=AH^2+HC^2\)

\(\Leftrightarrow CH^2=AC^2-AH^2=5^2-3^2=16\)

hay CH=4(cm)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+HB^2\)

\(\Leftrightarrow AB^2=3^2+2.25^2=14.0625\)

hay AB=3,75(cm)

Ta có: BH+CH=BC(H nằm giữa B và C)

nên BC=2,25+4=6,25(cm)

Chu vi của tam giác ABH là: 

\(C_{ABH}=AB+BH+HA=3.75+2.25+3=9\left(cm\right)\)

Chu vi của tam giác ACH là:

\(C_{ACH}=AC+CH+AH=5+3+4=12\left(cm\right)\)

Chu vi của tam giác ABC là:

\(C_{ABC}=AB+AC+BC=3.75+6.25+5=15\left(cm\right)\)

Bài 1: 

a: AB+AC=75-45=30(cm)

b: AB=(30+4):2=17(cm)

=>AC=13cm

\(S=17\cdot13=221\left(cm^2\right)\)

Bài 2: 

a: BC=67-47=20(cm)

b: \(S=\dfrac{15\cdot20}{2}=15\cdot10=150\left(cm^2\right)\)

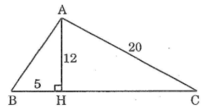
∆AHB có ∠(AHB) =90°

Theo định lý pitago, ta có:

AB2=AH2+HB2

= 122+52=169

Vậy AB = 13 cm

∆AHC có ∠(AHC) =90o

Theo định lý pitago, ta có:

AC2=AH2+HC2

HC2=AC2-AH2=202-122=400-144=256

Vậy HC = 16cm

Ta có: BC = BH + HC = 5 +16 = 21cm

Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

a, Áp dụng định lý Pitago:

`AB^2  + AC^2 = BC^2`

`=> 25 + AC^2 = 169`

`=> AC^2 = 144`

`=> sqrt 144  = 12`.

b. Áp dụng định lý Pytago ta có:

`AB^2 + AC^2 = BC^2`

`16 + 49 = BC^2`

`BC^2 = 65`

`BC  = sqrt 65`.

Áp dụng định lí Pitago trong tam giác ABC vuông tại A

AC = BC² + AB²

       = 13² + 5²    

        ^{= \(\sqrt{194}\)  = 14 cm}

Áp dụng định lí Pitago trong tam giác ABC cân tại A

BC = AB²  + AC²

       = 4²  + 7²  

       = \(\sqrt{65}\) = 8 cm