1=1khi nao

Những câu hỏi liên quan
Tìm m để hàm số sau có giới hạn khi x → 1:
f
x
x
2
+
x
-
2
1
-
x
+
m
x...
Đọc tiếp
Tìm m để hàm số sau có giới hạn khi x → 1: f x = x 2 + x - 2 1 - x + m x + 1 k h i x < 1 3 m x + 2 m - 1 k h i x ≥ 1
A. m = 2 3
B. m = 2 5
C. m = 3 2
D. m = 1 2
- Ta có:
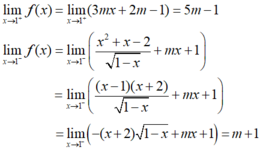
- Hàm số có giới hạn khi x → 1 khi và chỉ khi:
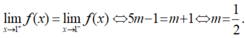
Chọn D.
Đúng 0
Bình luận (0)
Tìm m để hàm số sau có giới hạn khi x → 1.
f
x
x
2
+
x
-
2
1
-
x
+
m
x...
Đọc tiếp
Tìm m để hàm số sau có giới hạn khi x → 1.
f x = x 2 + x - 2 1 - x + m x + 1 k h i x < 1 3 m x + 2 m - 1 k h i x ≥ 1
A. 2 3
B. 2 5
C. 3 2
D. 1 2
Đáp án D
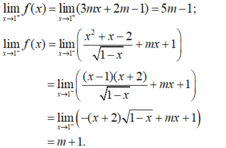
→ Hàm số có giới hạn khi x → 1 khi và chỉ khi:
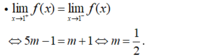
Đúng 0
Bình luận (0)
1+1khi nào mới =3
Xem thêm câu trả lời
1+1khi nào mới =3
Xem thêm câu trả lời
Tìm a để hàm số:
f
x
x
2
+
a
x
+
1
k
h
i
x
2...
Đọc tiếp
Tìm a để hàm số: f x = x 2 + a x + 1 k h i x > 2 2 x 2 - x + 1 k h i ≤ 2 có giới hạn tại x=2
A. 1
B. -1
C. 2
D. -2
Cho hàm số
y
f
x
x
+
1
k
h
i
x
0
x
2
-...
Đọc tiếp
Cho hàm số y = f x = x + 1 k h i x < 0 x 2 - 3 x + 1 k h i x ≥ 0 . Biết rằng hàm số y = f ( x ) có đồ thị (C) như hình vẽ bên. Khẳng định nào sau đây là sai?
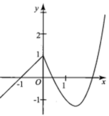
A. Hàm số đã cho không có đạo hàm tại điểm x = 0
B. Hàm số đã cho có 2 điểm cực trị
C. Hàm số đã cho liên tục trên R
D. Hàm số đã cho đồng biến trên R
Chọn D
Tại 1 điểm nào đó trên đồ thị mà đồ thị hàm số không có tiếp tuyến, khi đó hàm số không có đạo hàm tại điểm đó.
Đúng 0
Bình luận (0)
Tìm m để hàm số
h
x
x
3
+
1
x
+
1
k
h
i
x...
Đọc tiếp
Tìm m để hàm số h x = x 3 + 1 x + 1 k h i x < - 1 m x 2 - x + m 2 k h i x ≥ - 1 có giới hạn tại x = - 1 .
- Ta có:
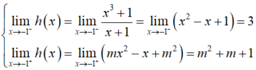
- Hàm số có giới hạn tại x = -1 khi và chỉ khi:
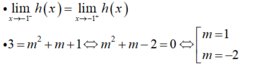
- Vậy để hàm số đã cho có giới hạn tại x = -1 khi m = 1 hoặc m = -2.
Đúng 0
Bình luận (0)
Tìm a để hàm số
f
(
x
)
x
2
-
1
x
-...
Đọc tiếp
Tìm a để hàm số f ( x ) = x 2 - 1 x - 1 k h i x ≠ 1 a k h i x = 1 liên tục tại điểm x0=1.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Chọn C
TXĐ: ![]() .
.
Ta có : ![]() .
.
![]() .
.
Hàm số ![]() liên tục tại điểm
liên tục tại điểm ![]() khi và chỉ khi
khi và chỉ khi ![]() .
.
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau tại
x
0
1
.
f
(
x
)
2
x
+
3
k
h
i
≥
1
x...
Đọc tiếp
Tính đạo hàm của hàm số sau tại x 0 = 1 . f ( x ) = 2 x + 3 k h i ≥ 1 x 3 + 2 x 2 - 7 x + 4 x - 1 k h i x < 1
A. 0
B. 4
C. 5
D. Đáp án khác
- Ta có:
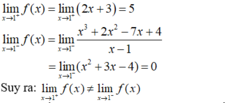
⇒ hàm số không liên tục tại x = 1 nên hàm số không có đạo hàm tại x 0 = 1 .
Chọn D.
Đúng 0
Bình luận (0)










