Bài 2 với ạ
Các bn ơi cho tui hỏi với dc ko ạ bài bài 2
D 23. 17 - 23.14 với ạ mình chưa bt bài này ạ giúp mình với ạ
giúp mình với ạ bài 1 với bài 2 ạ

Bài 2:
Ta có:\(2\sqrt{48}< 2\sqrt{49}\) ;
\(3\sqrt{27}>3\sqrt{25}\)
mà \(2\sqrt{49}< 3\sqrt{25}\left(14< 15\right)\)
\(\Rightarrow3\sqrt{27}>3\sqrt{25}>2\sqrt{49}>2\sqrt{48}\)
\(\Rightarrow3\sqrt{27}>2\sqrt{48}\)
b)
Ta có:\(\sqrt{50}+\sqrt{2}>\sqrt{49}+\sqrt{1}\)
\(\sqrt{50+2}< \sqrt{64}\)
mà \(\sqrt{49}+\sqrt{1}=\sqrt{64}\left(8=8\right)\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>8>\sqrt{50+2}\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>\sqrt{50+2}\)
bài 1câu b.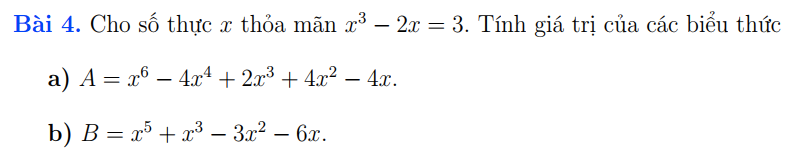
giúp em câu b với ạ.
và bài này ạ. bài 2: 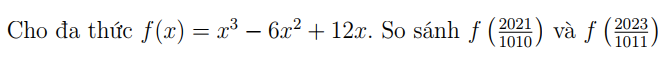
\(A=x^6-2x^4-2x^4+4x^2+2x^3-4x\\ A=x^3\left(x^3-2x\right)-2x\left(x^3-2x\right)+2\left(x^3-2x\right)\\ A=\left(x^3-2x\right)\left(x^3-2x+2\right)=3\left(3+2\right)=3\cdot5=15\\ B=x^5-2x^3+3x^3-6x-3x^2\\ =x^2\left(x^3-2x\right)+3\left(x^3-2x\right)-3x^2\\ =\left(x^3-2x\right)\left(x^2+3\right)-3x^2=3\left(x^2+3\right)-3x^2\\ =3x^2-3x^2+9=9\)
 giúp e với, có 2 bài thôi ạ, bài 1 toàn khoanh, còn bài 2 chia động từ ạ
giúp e với, có 2 bài thôi ạ, bài 1 toàn khoanh, còn bài 2 chia động từ ạ

3 A
4 D
5 A
6 C
7 C
8 A
9 A
10 C
11 C
12 A
13 A
14 B
15 A
16 D
17 D
18 C
19 D
20 D
21 C
22 C
23 C
24 C
25 C
Ex2
1 remember
2 read
3 be repaired
4 focus
5 not enter
6 apoligize
7 attend
8 sit
9 think
10 drive
11 be taken
12 reduce
13 allow
14 regulated
15 swim
16 monitor
17 out
18 be invited
19 send
20 work
mn giúp mih với ạ bài 2 với ạ
Bài 1:
a: 726314:29=25045(dư 9)
b: 172864:315=548,7746032
Giúp mình 1 trong 2 bài này với ạ. Nếu được thì giải 2 bài này giúp mk với. Mình đang cần gấp lắm ạ 😢
jimmmmmmmmmmmmmmmmmmmmmmmmmmm
he he he he he he
bài 1:
bn lấy giá trị của √(4^2-3,9^2) là dc
bài 2
AB+BC=2√(3^2+4^2)=??
Dạ mng xem giúp mình mấy bài trắc nghiệm làm đúng chưa với ạ , mng giúp mình luôn câu 5 bài 2 và câu 2 bài 3 ạ
Mình cảm ơn trước ạ


Bài 2
5 C
Bài 3
1 D
6 C
Còn lại ol r nhé
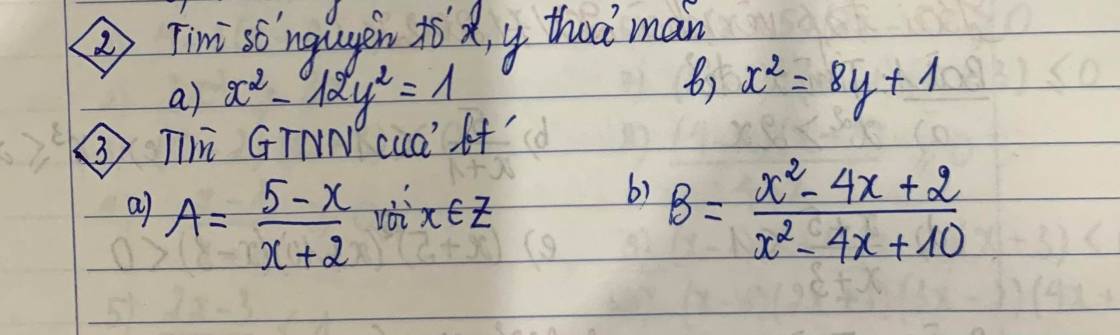 ai giúp em bài 2 với bài 3b với ạ
ai giúp em bài 2 với bài 3b với ạ
Bài 2:
a. $x^2=12y^2+1$ lẻ nên $x$ lẻ
Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$
$\Rightarrow 12y^2+1\equiv 1\pmod 8$
$\Rightarrow 12y^2\equiv 0\pmod 8$
$\Rightarrow y^2\equiv 0\pmod 2$
$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.
Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)
Bài 2:
b.
$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.
Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$
$\Rightarrow 2y=k(k+1)$
Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:
TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm)
TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý)
TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)
Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.
Bài 3:
a. $A=\frac{5-x}{x+2}=\frac{7-(x+2)}{x+2}=\frac{7}{x+2}-1$
Để $A$ min thì $\frac{7}{x+2}$ min
Điều này xảy ra khi $x+2$ là số nguyên âm lớn nhất
$\Rightarrow x+2=-1$
$\Rightarrow x=-3$. Khi đó: $A_{\min}=\frac{7}{-1}-1=-7-1=-8$
b.
$B=\frac{x^2-4x+10-8}{x^2-4x+10}=1-\frac{8}{x^2-4x+10}$
Để $B$ min thì $\frac{8}{x^2-4x+10}$ max
Điều này xảy ra khi $x^2-4x+10$ min
Mà: $x^2-4x+10=(x-2)^2+6\geq 6$ với mọi $x$
$\Rightarrow x^2-4x+10$ max = 6 khi $x=2$
Khi đó: $B_{\min}=1-\frac{8}{x^2-4x+10}=1-\frac{8}{2^2-4.2+10}=\frac{-1}{3}$
mọi người giúp 1 trong 2 bài này với ạ, bài nào cũng đx hết ạ
\(1,\) Ta có \(2022\equiv1\left(mod47\right)\)
\(\Rightarrow2022^{2021}\equiv1\left(mod47\right)\)
Vậy \(2022^{2021}:47\) dư 1
\(2,\) Thay \(x=1\) vào nhị thức, ta được \(\left(5x-6\right)^{2021}=\left(-1\right)^{2021}=-1\)
Vậy tổng các hệ số là \(-1\)
\(1,\left(a+b-2c\right)^3+\left(b+c-2a\right)^3+\left(c+a-2b\right)^3\)
Đặt \(a+b-2c=x;b+c-2a=y;c+a-2b=z\Leftrightarrow z=x+y\), pt trở thành:
\(x^3+y^3+z^3\\ =\left(x+y\right)^3-3xy\left(x+y\right)+z^3\\ =-z^3-3xy\left(-z\right)+z^3\\ =3xyz\\ =3\left(a+b-2c\right)\left(b+c-2a\right)\left(a+c-2b\right)\)
\(2,\left(a+b+c\right)^3+\left(a-b-c\right)^3+\left(b-c-a\right)^3+\left(c-a-b\right)^3\\ =8a^3-3\left(a+b+c\right)\left(a-b-c\right)\cdot2a-8a^3-3\left(b-c-a\right)\left(c-a-b\right)\left(-2a\right)\\ =-6a\left\{a^2-\left(b+c\right)^2-\left[\left(-a\right)^2-\left(b-c\right)^2\right]\right\}\\ =-6a\left[a^2-a^2+\left(b-c\right)^2-\left(b+c\right)^2\right]\\ =-6a\left(b-c+b+c\right)\left[b-c-\left(b+c\right)\right]=24abc\)



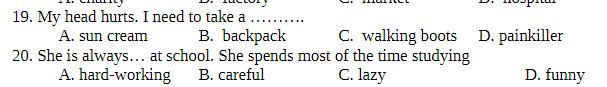
Cíu với, các bạn làm từng bài cũng được ạ :(( Làm mỗi bài 2 thôi ạ