
Làm giúp e bài 4 thui nha mọi ngươi ơi :333
Giúp mik gấp vs mn ơi! Trả lời bài 4 thui nha
Bài 4:
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
b: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA⊥BC
c: Xét ΔOBA vuông tại B có BA là đường cao
nên \(OH\cdot OA=OB^2=R^2\)
Mọi người giúp mình làm 1 bài thơ 4 chữ hoặc 5 chữ được không ạ? :333
~ Đề tài về: tình bạn, gia đình hoặc trường lớp ~
Giúp mình với nha, mình cần gấp
Cảm ơn trước ạ :>>>
Bạn em tên Dũng
Bạn rất đẹp trai
Quê ở Lào Cai
Nhà ở Quê Bái.
Bạn ấy rất tốt
Làm được nhiều thứ
Không hề trách cứ
Những ai có lỗi.
:))))))))))
mng ơi giúp mik bài này vs đề hơi sai chỗ R->B và câu e) -> câu d) nha
hình nha mng đừng để ý đường gạch ở giữa (lỡ tay thui)

Mọi người ơi giúp e làm bài này với
1. had lived /moved.
2. died /were performing.
3. was /haven't seen.
4. was cleaning /noticed.
5. finished /had been.
6. was crossing /caught.
7. was /booked.
8. hear /shouted.
9. had you read/ interrupted.
10. wanted/ had already done.
11. watched/ didn't realise.
12. tidied/ sat/ had.
13. Have you ever visited/ lived.
14. called/ saw.
15. came/ had forgotten.
mọi người ơi giúp mình bài này với , làm đc bài nào thì giúp mình nha :
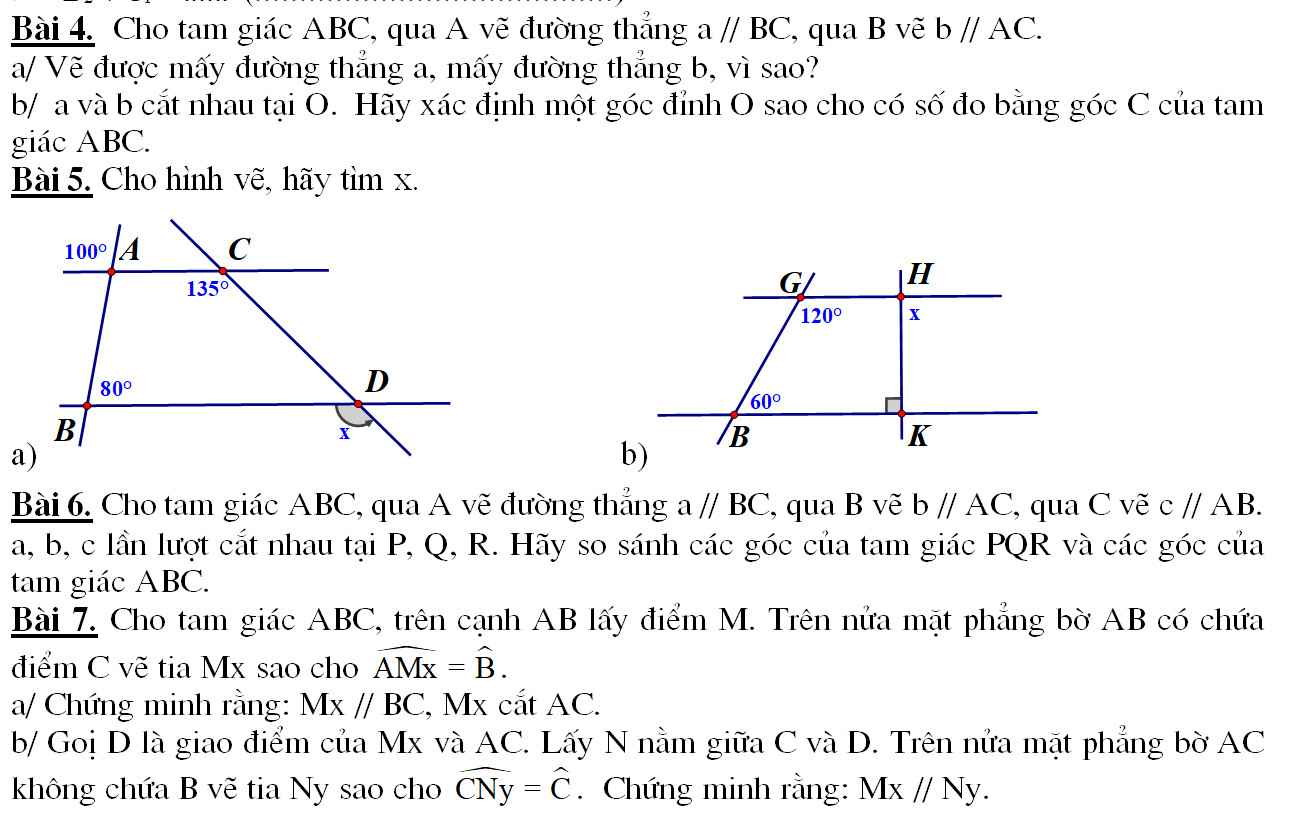
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
mọi người ơi giúp mình , ai làm đc bài nào thì giúp mình nha :

Vì đg thẳng c vuông góc với đg thẳng b
Đg thăng c vuông góc với đg thẳng a
=》a//b

mọi người ơi giúp mik với ai làm đc bài nào thì giúp mik nha
Tại sao các nước trên thế giới chế tạo vũ khí hạt nhân để làm gì
Giúp mk với mọi ngươi ơi
tui nghĩ : vì nó là nguồn năng lượng sạch đảm bảo sự phát triển bền vững trong việc thỏa mãn nhu cầu điện năng đang tăng mạnh trên toàn cầu. nghĩ thui ...ko chắc đâu
bạn ơi vũ khí hạt nhân rất nguy hiểm nên hiện nay nó đang phát triển rất chậm , họ chế tạo vũ khí đó để chuẩn bị cho một sự việc gì đó
Mọi người ơi giúp mình làm từ bài 44 đến 50 với nha mọi người mình cảm ơn nhiều
4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c
47. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{\left(a+b\right)^2}{c}+\dfrac{\left(b+c\right)^2}{a}+\dfrac{\left(c+a\right)^2}{b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+c}=\dfrac{\left[2\left(a+b+c\right)\right]^2}{a+b+c}=\dfrac{4\left(a+b+c\right)^2}{a+b+c}=4\left(a+b+c\right)\)(đpcm)
Đẳng thức xảy ra <=> a=b=c