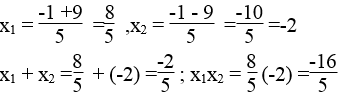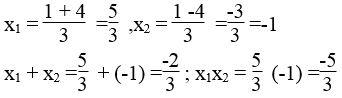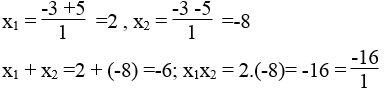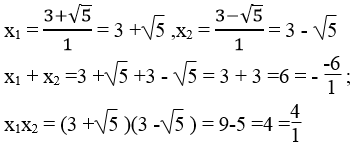Bài 2:

a: =>2x^2-4x+1=x^2+x+5

=>x^2-5x-4=0

=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)

b: =>11x^2-14x-12=3x^2+4x-7

=>8x^2-18x-5=0

=>x=5/2 hoặc x=-1/4

a. (3x - 1)² - (x + 3)² = 0

\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)

\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)

\(\Leftrightarrow4x+2=0\)  hoặc  \(2x-4=0\)

1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)

2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)

S=\(\left\{-\dfrac{1}{2};2\right\}\)

b. \(x^3=\dfrac{x}{49}\)

\(\Leftrightarrow49x^3=x\)

\(\Leftrightarrow49x^3-x=0\)

\(\Leftrightarrow x\left(49x^2-1\right)=0\)

\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)

\(\Leftrightarrow x=0\) hoặc  \(7x+1=0\) hoặc \(7x-1=0\)

1. x=0

2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)

3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)

*Cách khác:

a) Ta có: \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)

\(\Leftrightarrow\left(3x-1\right)^2=\left(x+3\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-1=-x-3\\3x-1=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-2\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)

Vậy: \(S=\left\{-\dfrac{1}{2};2\right\}\)

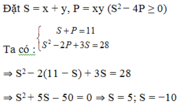
Khi S = 5 ⇒ P = 6 thì x, y là nghiệm của phương trình 

Khi S = −10 ⇒ P = 21 thì x, y là nghiệm của phương trình 

Vậy hệ có nghiệm (3; 2), (2; 3), (−3; −7), (−7; −3).

Đáp án cần chọn là: D

2 x − y = 3 x 2 + y = 5 ⇔ x 2 + 2 x = 8 2 x − y = 3 ⇔ x 2 + 2 x − 8 = 0    ( 1 ) y = 2 x − 3           ( 2 )

Giải (1):  Δ ' = 9  ;  x 1 = 2  ,  x 2 = − 4

Thay vào (2): Với  x = 2   t h ì   y = 2.2 − 3 = 1

Với x = − 4   t h ì   y = 2. ( − 4 ) − 3 = − 11

Vậy nghiệm của hệ phương trình là:  x , y ∈ 2 ; 1 , − 4 ; − 11

a) \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14y=-42\\2x+3y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x+3.\left(-3\right)=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x-9=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)

Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)

b) \(3x^2+4x=0\) 

\(\Leftrightarrow x\left(3x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)

Vậy phương trình có tập nghiệm là: \(S=\left\{0;-\dfrac{4}{3}\right\}\)

c) Đặt:  \(x^2=t\left(t\ge0\right)\)

\(\Rightarrow\) Ta có phương trình mới:

\(t^2-3t-4=0\) 

Ta có: a - b + c = 1 + 3 - 4 = 0

\(\Rightarrow t_1=-1\left(loại\right);t_2=4\left(TM\right)\)

\(\Rightarrow x=\pm2\)

Vậy tập nghiệm của phương trình là: S = {2; -2}

a, \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\left(1\right)\\6x-5y=27\left(2\right)\end{matrix}\right.\)

Lấy (1) - (2) ta được : \(14y=-15-27=-42\Leftrightarrow y=-3\)

\(\Rightarrow6x-27=-15\Leftrightarrow6x=12\Leftrightarrow x=2\)

Vậy \(\left(x;y\right)=\left(2;-3\right)\)

b, \(3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow x=0;x=-\dfrac{4}{3}\)

c, \(x^4-3x^2-4=0\Leftrightarrow x^4+x^2-4x^2-4=0\)

\(\Leftrightarrow x^2\left(x^2-4\right)+x^2-4=0\Leftrightarrow\left(x^2+1\right)\left(x-2\right)\left(x+2\right)=0\)

\(\Leftrightarrow x=\pm2;x^2+1>0\)

Vậy nghiệm của phương trình là x = -2 ; x = 2 

Phương trình 5x2 + 2x -16 =0 có hệ số a=5 ,b=2 c=-16

Ta có: Δ'=12 -5(-16) = 1 + 80 =81 >0

Δ' = 81 =9

Phương trình 3x2 -2x -5 =0 có hệ số a =3,b = -2, c = -5

Ta có: Δ'=(-1)2 -3(-5) = 1 + 15 =16 >0

Δ' = 16 =4

Phương trình 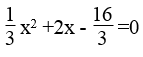 ⇔ x2 +6x – 16 = 0 có hệ số a = 1, b = 6, c = -16

Δ'=32 -1(-16) = 9 +16 =25 > 0

Δ' = 25 =5

Phương trình 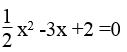 ⇔ x2 -6x +4 =0 có hệ số a=1,b=-6,c=4

Ta có: Δ'=(-3)2 -1.4 = 9 -4 =5 >0

Δ' = 5

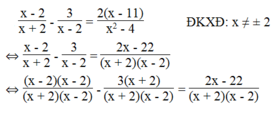
⇔ (x – 2)(x – 2) – 3(x + 2) = 2x – 22

⇔ x 2  – 2x – 2x + 4 – 3x – 6 = 2x – 22

⇔  x 2  – 2x – 2x – 3x – 2x + 4 – 6 + 22 = 0

⇔  x 2  – 9x + 20 = 0

⇔  x 2  – 5x – 4x + 20 = 0

⇔ x(x – 5) – 4(x – 5) = 0

⇔ (x – 4)(x – 5) = 0

⇔ x – 4 = 0 hoặc x – 5 = 0

x – 4 = 0 ⇔ x = 4

x – 5 = 0 ⇔ x = 5

Vậy phương trình có nghiệm x = 4 hoặc x = 5.