C/m : Trong tứ diện ; trực tâm , trọng tâm của các mặt, trực tâm của các mặt và các điểm chia các đoạn nối giao điểm các đường cao với đỉnh, theo tỉ số 2 : 1 kể từ đỉnh nằm trên một mặt cầu ( mặt cầu 12 điểm)
Trong hệ trục tọa độ Oxyz, cho tứ diện ABCD biết A(3;-2;m), B(2;0;0), C(0;4;0), D(0;0;3). Tìm giá trị dương của tham số m để thể tích tứ diện bằng 8.
A. m=8
B. m=4
C. m=12
D. m=6
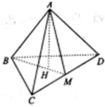
Cho tứ diện đều ABCD có cạnh bằng a. M là một điểm bất kì bên trong tứ diện. Tổng khoảng cách từ M đến các mặt của khối tứ diện là
A. Một đại lượng phụ thuộc vị trí của M
B. a 2 3
C. a 2
D. a 3
Chọn B.
Gọi x, y, z, t lần lượt là khoảng cách từ M đến các mặt phẳng (BCD), (CDA), (DAB), (ABC). Ta có

Cộng lại ta thu được (chú ý rằng)
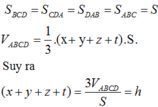
với h là độ dài đường cao của tứ diện đều ABCD. Ta có
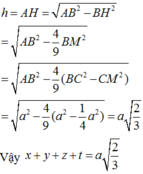
Cho tứ diện đều ABCD. Cho điểm M là điểm thuộc miền trong tam giác BCD, I, J, K lần lượt là hình chiếu của M xuống các mặt phẳng (ABC), (ACD), (ADB). Xác định vị trí của điểm M để khối tứ diện MIJK có thể tích lớn nhấ
Bài Toán :
Cho tứ giác ABCD. Hãy dựng điểm M trong tứ giác sao cho :
Điểm M nối tới trung điểm của 4 cạnh tứ giác chia tứ giác thành 4 hình có diện tích bằng nhau
cho tứ diện ABCD, điểm I thuộc cạnh AB, J là điểm trong tam giác BCD, K là điểm trong tam giác ACD
a) Tìm giao điểm của IK và (BCD)
b) Tìm giao tuyến của (IJK) và (ABC)
c) Tìm giao tuyến của (IJK) và các mặt phẳng còn lại của tứ diện
Lởi giải:
a)
Gọi $E$ là giao $AK,CD$. Ta thấy $E\in CD\Rightarrow BE\subset (BCD)$
Gọi $M$ là giao $IK, BE$. Khi đó:
$M\in IK$. $M\in BE\Rightarrow M\in (BCD)$. Do đó $M=IK\cap (BCD)$
b)
Gọi $F$ là giao $DK,AC$, $H$ là giao $DJ, BC$
$\Rightarrow FH\subset (ABC)$. Lấy $G$ là giao điểm $FH, JK$ thì ta thấy:
$G\in FH\Rightarrow G\in (ABC)$
$G\in JK\Rightarrow G\in (IJK)$
$I\in AB\Rightarrow I\in (ABC)$
$I\in (IJK)$
$\Rightarrow GI$ là giao tuyến của $(IJK)$ và $(ABC)$
c)
Giao tuyến của $(IJK)$ và $(ACD)$
Gọi $L$ là giao $IG, AC$.
$L\in IG\Rightarrow L\in (IJK)$
$L\in AC\Rightarrow L\in (ACD)$
Mà $E\in IK\Rightarrow E\in (IJK)$
$E\in CD\Rightarrow E\in (ACD)$
Do đó $EL$ là giao tuyến của $(IJK)$ và $(ACD)$
------------------
Giao tuyến của $(IJK)$ và $(ABD)$
Gọi $P$ là giao điểm $EJ$ và $BD$
$P\in BD\Rightarrow P\in (ABD)$
$P\in EJ\Rightarrow P\in (IJK)$
$I\in (IJK)$ và $I\in (ABD)$
$\Rightarrow PI$ là giao tuyến $(ABD)$ và $(IJK)$
------------------
Giao tuyến $(IJK)$ và $(BCD)$
$E\in IK\Rightarrow E\in (IJK)$
$E\in CD\Rightarrow E\in (BCD)$
$P\in (IJK)$ và $P\in BD\Rightarrow P\in (BCD)$
Do đó $PE$ là giao tuyến $(IJK)$ và $(BCD)$
Bạn tự vẽ hình.
cho tứ diện ABCD và điểm M nằm trong tứ diện, qua M dựng các mặt phẳng (a) song song (BCD), (b) song song (ACD), (c) song song (ABD), (d) song song (ABC). Biết (a) cắt AB tại E, (b) cắt BC tại F, (c) cắt CD tại P, (d) cắt AD tại Q
cmr: \(\sqrt{\dfrac{EA}{EB}}+\sqrt{\dfrac{FB}{FC}}+\sqrt{\dfrac{PC}{PD}}+\sqrt{\dfrac{QD}{QA}}\ge4\sqrt{3}\)
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M là một điểm thuộc miền trong của khối tứ diện tương ứng. Giá trị lớn nhất của tích các khoảng cách từ điểm M đến bốn mặt phẳng của tứ diện đã cho là
A. a 4 521
B. a 4 576
C. a 4 6 81
D. a 4 6 324
Chọn đáp án B
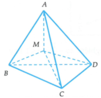
Gọi r1, r2, r3, r4 lần lượt là khoảng cách từ điểm M đến các mặt phẳng (BCD), (ACD), (ABD), (ABC)
Gọi S là diện tích một mặt của tứ diện đều thì
Thể tích tứ diện đều ABCD là V A B C D = a 3 2 12
Ta có V A B C D = V M . B C D + V M . A C D + V M . A B D + V M . A B C
![]()
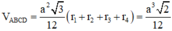
Áp dụng bất đẳng thức Cauchy cho các số dương ta có:
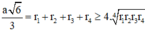
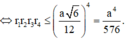
Dấu “=” xảy ra khi và chỉ khi
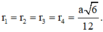
Cho tứ giác lồi ABCD. Tìm tập hợp điểm O nằm trong tứ giác sao cho hai tứ giác OBCD và OBAD có diện tích bằng nhau. ( k yêu cầu chứng minh phần đảo )
cho tứ diện abcd m,n nằm trong tam giá abd,acd, thiết diện tứ giác abcd với mặt phẳng (dmn) là hình gì
Cho tứ diện ABCD. Điểm M thuộc đoạn AC M (khác A M, khác C). Mặt phẳng ( α ) đi qua M song song với AB và AD. Thiết diện của với tứ diện ABCD là hình gì?
A. Hình tam giác.
B. Hình bình hành.
C. Hình vuông
D. Hình chữ nhật.