Giả sử a và b là hai số nguyên dương sao cho (a + 2b)(a - b) = 10. Tìm giá trị của 2a - b ?

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của a + b, nếu a và b là hai số nguyên dương và \(\frac{1}{2a}+\frac{1}{3a}+\frac{1}{4a}=\frac{1}{b^2-2b}\)
+ cách giải
Ta có:
\(\frac{1}{2a}+\frac{1}{3a}+\frac{1}{4a}=\frac{1}{b^2-2b}\)
\(\Leftrightarrow13b^2-26b-12a=0\)
\(\Leftrightarrow12\left(a+b\right)=13b^2-14b\)
\(\Leftrightarrow a+b=\frac{13b^2-14b}{12}\)
\(\Leftrightarrow a+b=b^2-b+\frac{b^2-2b}{12}=b^2-b+\frac{b\left(b-2\right)}{12}\)
Dễ thấy b phải là số chẵn (1)
để \(\frac{b\left(b-2\right)}{2.2.3}\) nguyên thì
\(\Rightarrow\orbr{\begin{cases}b⋮3\\b-2⋮3\end{cases}}\)(2)
Từ (1) và (2) \(\Rightarrow\orbr{\begin{cases}b=6k\\b-2=6k\end{cases}\left(k\ge1\right)}\)
Với \(b=6k\) thế vào ta được
\(a+b=\frac{13\left(6k\right)^2-14.\left(6k\right)}{12}=36k^2-7k\)
Dễ thấy hàm số \(f\left(k\right)=39k^2-7k\) là hàm đồng biết với \(k\ge1\)
Từ đây ta có a + b nhỏ nhất khi k nhơ nhất hay \(k=1\)
\(\Rightarrow\hept{\begin{cases}b=6\\a=26\\a+b=32\end{cases}}\)
Tương tự cho trường hợp \(b-2=6k\) sẽ tìm được GTNN của a + b
PS: Vì m thích làm sự đơn điệu của hàm số thôi. Nếu các b có cách khác thì cứ làm cho gọn nhé :)
Đúng 0
Bình luận (0)
\(\Rightarrow a=26\), \(b=6\)Còn cách làm thì giống như Bạn alibaba nguyễn đó bạn
~ Chúc bạn học giỏi ~~~
Đúng 0
Bình luận (0)
Giả sử a và b là số nguyên dương và bốn số a + b, a − b, × b, ÷ b là khác nhau và tất cả đều là số nguyên dương. Giá trị nhỏ nhất có thể của a + b là gì?
a) Cho a,b,c,d >0 và dãy tỉ số :\(\dfrac{2b+c-a}{a}=\dfrac{2c-b+a}{b}=\dfrac{2a+b-c}{c}\)
Tính :P=\(\dfrac{\left(3a-2b\right)\left(3b-2c\right)\left(3c-2a\right)}{\left(3a-c\right)\left(3b-a\right)\left(3c-b\right)}\)
b)Tìm giá trị nguyên dương của x và y sao cho:\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\)
hộ tui vs các chế
b.\(ĐK:x;y\in Z^+;x;y\ne0\)
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{5}{x}+\dfrac{5}{y}=1\)
\(\Leftrightarrow\dfrac{5}{x}=1-\dfrac{5}{y}\)
\(\Leftrightarrow\dfrac{5}{x}=\dfrac{y-5}{y}\)
\(\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{y-5}\)
\(\Leftrightarrow x=\dfrac{5y}{y-5}\)
\(\Leftrightarrow x=5+\dfrac{25}{y-5}\) ( bạn chia \(5y\) cho \(y-5\) ý )
Để x;y là số nguyên dương thì \(25⋮y-5\) hay \(y-5\in U\left(25\right)=\left\{\pm1;\pm5;\pm25\right\}\)
TH1:
\(y-5=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=30\end{matrix}\right.\) ( tm ) ( bạn thế y=6 vào \(x=5+\dfrac{25}{y+5}\) nhé )
Xét tương tự, ta ra được nghiệm nguyên dương của phương trình:
\(\left\{{}\begin{matrix}x=30\\y=6\end{matrix}\right.\) \(\left\{{}\begin{matrix}x=10\\y=10\end{matrix}\right.\) \(\left\{{}\begin{matrix}x=6\\y=30\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Giả sử a và b là số nguyên dương và bốn số a + b, a − b, × b, ÷ b là khác nhau và tất cả đều là số nguyên dương. Giá trị nhỏ nhất có thể của a + b là gì?
\(a,b\)nguyên dương nên hiển nhiên \(a+b,a\times b\)nguyên dương. \(a-b\)nguyên dương khi \(a>b\).
\(a\times b,a\div b\)có giá trị khác nhau nên \(b\ne1\).
Với \(b=2\): xét các giá trị của \(a\)để \(a\div b\)nguyên dương.
- \(a=2\): \(a-b=0\)không thỏa mãn.
- \(a=4\): \(a-b=a\div b=2\)không thỏa mãn.
- \(a=6\): thỏa mãn. Khi đó \(a+b=8\).
Với \(b\ge3\)thì để thỏa mãn thì \(a\ge2b\)khi đó \(a+b\ge3b\ge9>8\).
Vậy giá trị nhỏ nhất của \(a+b\)là \(8\).
tìm giá trị lớn nhất của biểu thức sau biết a,b,c là số nguyên dương và a+b+c=2 \(\sqrt{2a+bc}+\sqrt{2b+ac}+\sqrt{2c+ab}\)
\(\sqrt{2a+bc}+\sqrt{2b+ca}+\sqrt{2c+ab}\)
\(=\sqrt{a\left(a+b+c\right)+bc}+\sqrt{b\left(a+b+c\right)+ca}+\sqrt{c\left(a+b+c\right)+ab}\)
\(=\sqrt{\left(a+b\right)\left(a+c\right)}+\sqrt{\left(b+a\right)\left(b+c\right)}+\sqrt{\left(c+a\right)\left(c+b\right)}\)
\(\le\frac{a+b+a+c}{2}+\frac{b+a+b+c}{2}+\frac{c+a+c+b}{2}\)
\(=2\left(a+b+c\right)=4\)
Dấu = xảy ra khi \(a=b=c=\frac{2}{3}\)
Đúng 0
Bình luận (0)
Giả sử
m
-
a
b
,
a
,
b
∈
Z
+
,
(
a
,
b
)
1
là giá trị thực của tham số m để đường thẳng
d
:
y
-
3
x
+
m
cắt đồ thị hàm số
y
2
a...
Đọc tiếp
Giả sử m = - a b , a , b ∈ Z + , ( a , b ) = 1 là giá trị thực của tham số m để đường thẳng d : y = - 3 x + m cắt đồ thị hàm số y = 2 a + 1 x - 1 tại hai điểm phân biệt A,B sao cho trọng tâm tam giác OAB thuộc đường thẳng ∆ : x - 2 y - 2 = 0 với O là gốc tọa độ. Tính a+2b
A. 2
B. 5
C. 11
D. 21
Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
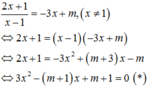
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
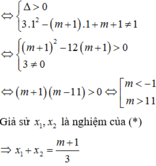

Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biêu thức \(P=\frac{a}{b+2c}+\frac{b}{c+2a}+\frac{c}{a+2b}\) với a,b,c là các số dương sao cho abc=1
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel:
\(P=\frac{a^2}{ab+2ca}+\frac{b^2}{bc+2ab}+\frac{c^2}{ca+2bc}\ge\frac{\left(a+b+c\right)^2}{3\left(ab+bc+ca\right)}\ge1\)
Cộng thêm giả thiết abc=1, suy ra dấu "=" xảy ra khi \(a=b=c=1\)
Tìm tất cả bộ ba số nguyên dương (a,b,c) sao cho (a+b+c)^2-2a+2b là số chính phương
Cho a, b là 2 số thực dương thỏa mãn a + b ab. Tìm giá trị nhỏ nhất của biểu thức
P
1
a
2
+
2
a
+
1
b
2
+
2
b
+
1
+...
Đọc tiếp
Cho a, b là 2 số thực dương thỏa mãn a + b = ab. Tìm giá trị nhỏ nhất của biểu thức P = 1 a 2 + 2 a + 1 b 2 + 2 b + 1 + a 2 1 + b 2
Áp dụng bất đẳng thức trên ta có ( 1 + a 2 ) ( 1 + b 2 ) ≥ 1 + a b = 1 + a + b (1)
Với mọi x, y > 0, áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
1 x + 1 y ( x + y ) ≥ 2 1 x . 1 y .2 x y = 4 ⇒ 1 x + 1 y ≥ 4 x + y (2)
Áp dụng (1) và (2) ta có:
P ≥ 4 a 2 + 2 a + b 2 + 2 b + 1 + a + b = 4 a 2 + b 2 + 2 a b + 1 + a + b = 4 ( a + b ) 2 + a + b 8 + 7 ( a + b ) 8 + 1
Áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
a + b = a b ≤ ( a + b ) 2 4 ⇒ ( a + b ) 2 ≥ 4 ( a + b ) ⇒ a + b ≥ 4
Áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
4 ( a + b ) 2 + a + b 16 + a + b 16 ≥ 3 4 ( a + b ) 2 . a + b 16 . a + b 16 3 = 3 4 ⇒ P ≥ 3 4 + 7 8 .4 + 1 = 21 4
Dấu bằng xảy ra khi a = b = 2. Vậy giá trị nhỏ nhất của P là 21/4
Đúng 0
Bình luận (0)
















