Giair hệ phương trình hepllllllllll
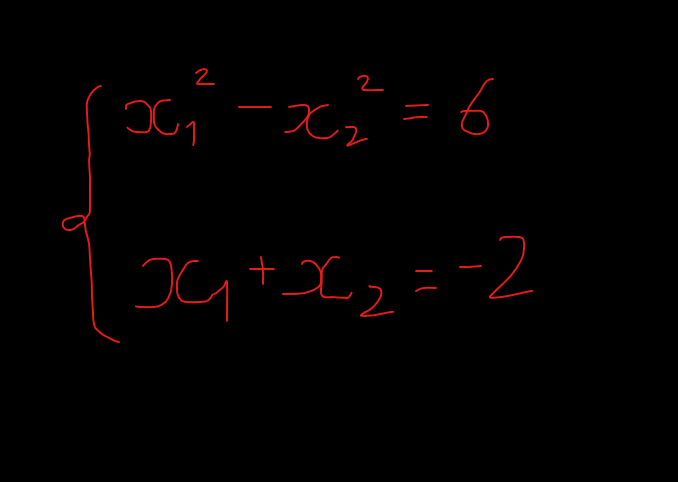
Giair hệ phương trình sauu
: {4x-2y=-52x+3y=4
Giải phương trình 4x - 2y = -5, ta có: \(\Rightarrow x=-\frac{5}{4}+\frac{1}{2}y\)
Thế giá trị đã có vào 2x + 3y =4, ta có: \(2\left(-\frac{5}{4}+\frac{1}{2}y\right)+3y=4\)
\(\Leftrightarrow-\frac{5}{2}+y+3y=4\)
\(\Leftrightarrow4y=\frac{13}{2}\Rightarrow y=\frac{13}{8}\)
Thay giá trị của y vào phương trình \(x=-\frac{5}{4}+\frac{1}{2}\times\frac{13}{8}\)
\(\Rightarrow x=-\frac{7}{16}\)
Giair Hệ phương trình nghiệm nguyên : \(\left\{{}\begin{matrix}5x+3y+\dfrac{z}{3}=100\\x+y+z=100\end{matrix}\right.\)
\(\left\{{}\begin{matrix}15x+9y+z=300\\x+y+z=100\end{matrix}\right.\)
\(\Rightarrow14x+8y=200\Rightarrow7x+4y=100\)
\(\Leftrightarrow7x=4\left(25-y\right)\)
Do 7 và 4 nguyên tố cùng nhau \(\Rightarrow x⋮4\Rightarrow x=4k\)
\(\Rightarrow y=25-7k\)
\(z=100-\left(x+y\right)=3k+75\)
Vậy nghiệm của pt là \(\left(x;y;z\right)=\left(4k;-7k+25;3k+75\right)\) với \(k\in Z\)
Giair Hệ phương trình nghiệm nguyên : \(\left\{{}\begin{matrix}x+y+z=3\\x^3+y^3+z^3=3\end{matrix}\right.\)
Lời giải:
Theo hằng đẳng thức đáng nhớ:
$x^3+y^3+z^3=(x+y+z)^3-3(x+y)(y+z)(x+z)$
$\Leftrightarrow 3=27-3(x+y)(y+z)(x+z)$
$\Leftrightarrow (x+y)(y+z)(x+z)=8$Đặt $(x+y,y+z,x+z)=(a,b,c)$ thì $abc=8$ và $a+b+c=6$Do $a+b+c=6>0$ nên $(a,b,c)$ sẽ là 3 số dương hoặc $1$ dương $2$ âm.
TH1: $a,b,c$ đều dương.
Áp dụng BĐT AM-GM: $a+b+c\geq 3\sqrt[3]{abc}=3\sqrt[3]{8}=6$
Dấu "=" xảy ra khi $a=b=c=2$
$\Leftrightarrow x+y=y+z=x+z=2\Leftrightarrow x=y=z=1$
TH2: $a,b,c$ có 1 số dương 2 số âm. Giả sử $a$ dương và $b,c$ âm.
$a+b+c=6$ nên $a>6$. Mà $abc=8$ nên $a=8$
$\Rightarrow bc=1$ và $b+c=-2$
$\Rightarrow b=c=-1$
$\Rightarrow x=y=4; z=-5$
Vậy $(x,y,z)=(1,1,1); (4,4,-5)$ và hoán vị.
Giair hệ phương trình:\(\hept{\begin{cases}|x-1|+|y-5|=1\\|x-1|-y=-5\end{cases}}\)
Đặt \(|x-1|=z\ge0\)
Ta có hệ:\(\hept{\begin{cases}z+|y-5|=1\\z-y=-5\end{cases}}\)
\(-TH1:\)
Nếu \(y< 5\) ta có: \(\hept{\begin{cases}z-y=-4\\z-y=-5\end{cases}}\)
Hệ này vô nghiệm
\(-TH2:\)
Nếu \(y\ge5\) ta có:\(\hept{\begin{cases}z+y=6\\z-y=-5\end{cases}}\)
Giải hệ này ta có: \(\hept{\begin{cases}z=\frac{1}{2}\\y=\frac{11}{2}\end{cases}}\)
\(z=|x-1|=\frac{1}{2}\Rightarrow x-1=\pm\frac{1}{2}\)
Do đó: \(x=\frac{3}{2}\)hoặc\(x=\frac{1}{2}\)
Vậy hệ đã cho có hai nghiệm là \(\left(\frac{3}{2};\frac{11}{2}\right)\)và\(\left(\frac{1}{2};\frac{11}{2}\right)\)
Giair hệ phương trình: \(\hept{\begin{cases}x^3-y^3=4.\left(4x-y\right)\\y^2-5x^2=4\end{cases}}\)
giair hệ phương trình:
\(\hept{\begin{cases}\sqrt{x-1}+\sqrt{y^2-2y+4}\\\sqrt{x-4}+y=3\end{cases}}=4\)
ĐKXĐ: \(x\ge4\)
\(\hept{\begin{cases}\sqrt{x-1}+\sqrt{y^2-2y+4}=4\\\sqrt{x-4}+y=3\left(1\right)\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}\sqrt{x-1}=4-\sqrt{y^2-2y+4}\\\sqrt{x-4}=3-y\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\left(\sqrt{x-1}\right)^2=\left(4-\sqrt{y^2-2y+4}\right)^2\\\left(\sqrt{x-4}\right)^2=\left(3-y\right)^2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x-1=16-8\sqrt{y^2-2y+4}+y^2-2y+4\\x-4=y^2-6y+9\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=-8\sqrt{y^2-2y+4}+y^2-2y+21\\x=y^2-6y+13\end{cases}}\)
\(\Rightarrow y^2-2y+21-8\sqrt{y^2-2y+4}=y^2-6y+13\)
\(\Leftrightarrow4y+8=8\sqrt{y^2-2y+4}\)\(\Leftrightarrow y+2=2\sqrt{y^2-2y+4}\)
\(\Rightarrow\left(y+2\right)^2=\left(2\sqrt{y^2-2y+4}\right)^2\Leftrightarrow y^2+4y+4=4y^2-8y+16\)
\(\Leftrightarrow3y^2-12y+12=0\Leftrightarrow y^2-4y+4=0\Leftrightarrow\left(y-2\right)^2=0\Leftrightarrow y-2=0\Leftrightarrow y=2\)
Thay y=2 vào (1) suy ra \(\sqrt{x-4}+2=3\Leftrightarrow\sqrt{x-4}=1\Leftrightarrow x-4=1\Leftrightarrow x=5\left(tmdk\right)\)
Vậy (x;y)=(5;2)
Giair hệ phương trình:
\(\hept{\begin{cases}\sqrt{x-1}+\sqrt{y-1}=3\\xy+x+y=x^3-2y^2\end{cases}}\)
Cho hệ phương trình \(\hept{\begin{cases}x+\left(m-1\right)y=2\\mx-y=1\end{cases}}\)(I)
Giair hệ phương trình (I)với m =2Tìm các giá trị của m để (I0 có nghiệm (x;y) thỏa mãn x>0 và y<0Giair hệ phương trình \(\hept{\begin{cases}1+\sqrt{y-1}=\frac{1}{y^2}-\left(x+z\right)^2\\x^2+y^2=2y\end{cases}}\)