Do 2 đường cao BD và CE cắt nhau tại H => H là trực tâm của tam giác ABC. Nối A với H sao cho AH cắt BC tại F, ta có AF là đường cao thứ 3 của tam giác ABC => \(AF\perp BC\)

Vì \(\Delta ABF\) vuông tại D \(\Rightarrow\widehat{BAF}+\widehat{ABF}=90^0\) hay \(\widehat{ABF}=\widehat{HAE}\) (1)

\(\Delta BEC\) vuông tại E \(\Rightarrow\widehat{BCE}+\widehat{CBE}=90^0\) hay \(\widehat{ABF}+\widehat{KCB}=90^0\) (2)

Từ (1) và (2) => \(\widehat{HAE}=\widehat{KCB}\) (3)

Ta dễ chứng minh được \(\Delta KAE=\Delta HAE\left(c-g-c\right)\)

\(\Rightarrow\widehat{KAE}=\widehat{HAE}\) hay \(\widehat{KAB}=\widehat{HAE}\) (4)

Từ (3) và (4) \(\Rightarrow\widehat{KAB}=\widehat{KCB}\)

Vậy...

AH cắt BC tại M.

Xét \(\Delta ABC\) có 2 đường cao BD và CE cắt nhau tại H

=> H là trực tâm của tam giác ABC

=> \(AH⊥BC\)

=> \(\Delta ABM\)vuông tại M

=> \(\widehat{BAM}+\widehat{ABM}=90^o\)

Mà \(\widehat{KCB}+\widehat{ABM}=90^o\)

Nên \(\widehat{BAM}=\widehat{KCB}\)

Ta có: AK = AH ( A thuộc đường trung trực của đoạn HK)

=> \(\Delta AKH\)cân tại A

Mà AE là đường trung tuyến nên cũng là đường phân giác

=> \(\widehat{KAB}=\widehat{BAM}\)

Mà \(\widehat{KCB}=\widehat{BAM}\)

Nên \(\widehat{KAB}=\widehat{KCB}\)\(\left(đpcm\right)\)

Nhật Tân

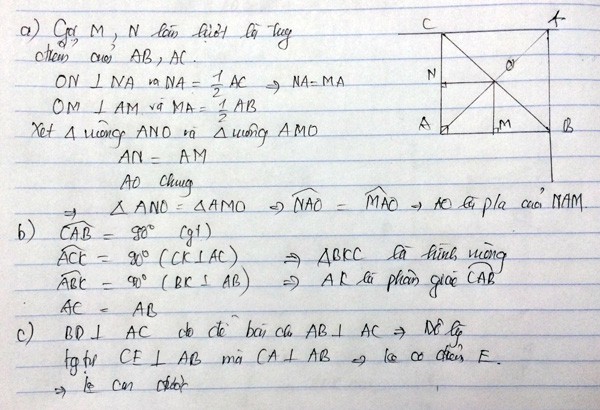
p/s: kham khảo

đề thiếu

nhầm tiếp, phải là;

a) Tam giác ABD=ACE.

xin lỗi lần 2

a)Xét △ABD và △ACE:

góc ADB = góc AEC = 90^o (BD vuông góc AC, CE vuông góc AB)

AB = AC (ΔABC cân tại A)

A là góc chung

Vậy △ABD = △ACE (ch.gn)

b) Ta có: △ABD = △ACE (cmt)

=>AD = AE (các cặp cạnh tương ứng)

=>△AED cân tại A

c) cho AF nằm trên AH sao cho AF\(\perp\)ED tại F

Xét △AFE và △AFD

góc AFE = góc AFD = 90^o (AF\(\perp\)ED tại F)

AE = AD (cmt)

AF là cạnh chung

Vậy △AFE = △AFD (ch.cgv)

=>FE = FD (các cặp cạnh tương ứng)

=> F là trung điểm của ED

Vì AF nằm trên AH

=> AH đi qua trung điểm của AE và AH\(\perp\)ED

=>AH là đường trung trực của ED

d)Xét ΔECB và\(\Delta\)DBC

góc CEB = góc BDC = 90^o ( BD vuông góc AC, CE vuông góc AB)

CB là cạnh chung

góc EBC = góc DCB (ΔABC cân tại A)

vậy ΔECB = \(\Delta\)DBC (ch.gn)

=> góc ECB = góc DBC (các cặp góc tương ứng)

Xét ΔCDB và ΔCDK

DB = DK (gt)

góc CDB = góc CDK = 90^o (gt)

DC là cạnh chung

Vậy ΔCDB = ΔCDK (c.g.c)

=> góc CBD = góc CKD (các cặp góc tương ứng)

Mà góc CBD = góc ECB (cmt)

=> góc ECB=DKC

tự kẻ hình

a) xét tam giác BEC và tam giác CDB có

BC chung

BEC=CDB(=90 độ)

ABC=ACB( tam giác ABC cân A)

=> tam giác BEC= tam giác CDB(ch-gnh)

=> BD=CE( hai cạnh tương ứng)

b) từ tam giác BEC= tam giác CDB=> DBC=ECB(hai góc tương ứng)

=> tam giác HBC cân H

c) đặt O là giao điểm của AH với BC

vì AH,BD,CE cùng giao nhau tại H mà BD, CE là đường cao=> AH là đường cao ( 3 đường cao cùng đi qua một điểm)

vì HBC cân H=> HB=HC

xét tam giác HOB và tam giác HOC có

HB=HC(cmt)

HBO=HCO(cmt)

HOB=HOC(=90 độ)

=> tam giác HOB= tam giác HOC(ch-gnh)

=> BO=CO( hai cạnh tương ứng)

=> AH là trung trực của BC

d) xét tam giác CDB và tam giác CDK có

BD=DK(gt)

CDB=CDK(=90 độ)

DC chung

=> tam giác CDB= tam giác CDK(cgc)

=> CBD=CKD( hai cạnh tương ứng)

mà CBD=BCE=> CKD=BCE