Cho 2 góc xOy và x^Oy là 2 góc nhọn và Ox//O^x^, Oy//O^y^. Chứng minh xOy=x^O^y^
Những câu hỏi liên quan
Chứng minh rằng
a) Nếu 2 góc xOy và góc x'O'y' cùng nhọn hoặc cùng tù có Ox vuông góc với Ox' và Oy vuông góc với Oy' thì góc xOy = góc x'O'y' b) Nếu góc xOy nhọn; góc x'O'y' tù và có Ox vuông góc với Ox' Oy vuông góc với Oy' thì góc xOy + góc x'O'y' = 180 độ
Chứng minh rằng :a) Nếu 2 góc xOy và góc xOy cùng nhọn hoặc cùng tù có Ox vuông góc với Ox và Oy vuông góc với Oy thì góc xOy góc xOy b) Nếu góc xOy nhọn; góc xOy tù và có Ox vuông góc với Ox Oy vuông góc với Oy thì góc xOy + góc xOy 180 độ
Đọc tiếp
Chứng minh rằng :
a) Nếu 2 góc xOy và góc x'O'y' cùng nhọn hoặc cùng tù có Ox vuông góc với Ox' và Oy vuông góc với Oy' thì góc xOy = góc x'O'y'
b) Nếu góc xOy nhọn; góc x'O'y' tù và có Ox vuông góc với Ox' Oy vuông góc với Oy' thì góc xOy + góc x'O'y' =180 độ
a) tham khảo trên trang này:
https://lazi.vn/edu/exercise/748977/chung-minh-rang-neu-2-goc-xoy-va-goc-xoy-cung-nhon-hoac-cung-tu-co-ox-vuong-goc-voi-ox-va-oy-vuong-goc-voi-oy-thi-goc-xoy-goc-xoy#:~:text=B%C3%A0i%20t%E1%BA%ADp-,Ch%E1%BB%A9ng%20minh%20r%E1%BA%B1ng%20%3A%20N%E1%BA%BFu%202%20g%C3%B3c%20xOy%20v%C3%A0%20g%C3%B3c%20x%27O%27y%27%20c%C3%B9ng%20nh%E1%BB%8Dn%20ho%E1%BA%B7c%20c%C3%B9ng%20t%C3%B9%20c%C3%B3%20Ox%20vu%C3%B4ng%20g%C3%B3c%20v%E1%BB%9Bi%20Ox%27%20v%C3%A0%20Oy%20vu%C3%B4ng%20g%C3%B3c%20v%E1%BB%9Bi%20Oy%27%20th%C3%AC%20g%C3%B3c%20xOy%20%3D%20g%C3%B3c%20x%27O%27y%27,-Lan%20Nguy%E1%BB%85n%20%7C%20%20Chat
Đúng 0
Bình luận (0)
Chứng minh : Nếu 2 góc nhọn xOy và x'Oy' có Ox//O'x' và Oy//O'y' thì xOy=x'Oy'
Sửa đề: 2 góc nhọn xOy và x'O'y'
Gọi A là giao của Oy và O'x'
Vì Ox//O'x' nên \(\widehat{xOy}=\widehat{yAx'}\) (đồng vị)
Mà Oy//O'y' nên \(\widehat{yAx'}=\widehat{x'O'y'}\) (đồng vị)
Vậy \(\widehat{xOy}=\widehat{x'O'y'}\)
Đúng 1
Bình luận (0)
chứng minh rằng "nếu hai góc nhọn xOy và x'O'y'có Ox//O'x' Oy//O'y' thì xOy = x'O'y' (O' nằm trong góc xOy )
cho góc xoy và góc x phẩy o phẩy y phẩy là góc nhọn hoặc tù có: ox song o x phẩy và oy song song o phẩy y phẩy
c minh rằng góc xoy = góc x phẩy o phẩy y phẩy
chứng minh rằng : nếu hai góc xO'y và x'Oy' có Ox // O'x' , Oy//O'y' thì góc xOy = x'Oy' nếu cả hai góc cùng là góc nhọn hoặc cả hai góc cùng là góc tù , chúng bù nhau nếu góc này nhọn, góc kia tù
CMR: Nếu 2 góc nhọn xOy và x'O'y' có Ox//O'x' Oy//O'y' thì góc xOy = góc x'O'y'
Cho hai góc nhọn xOy và x'O'y' có các cạnh tương ứng Ox // O'x' , Oy // O'y'. Vẽ các tia Oz và O'z' lần lượt là phân giác của góc xOy và x'O'y'. Chứng tỏ :
a) Hai góc xOy và x'O'y' bằng nhau.
b) Oz // O'z'.
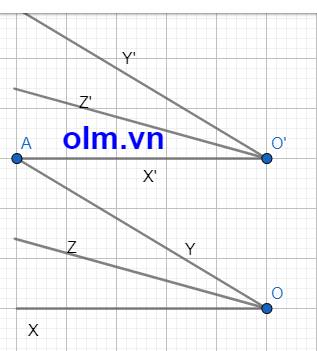
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
Đúng 0
Bình luận (0)
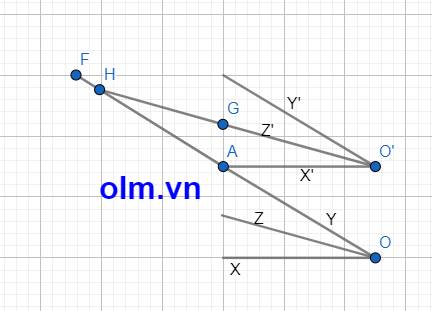
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)
Đúng 0
Bình luận (0)
Cho 2 góc tù Xoy và x'o'y' như hình bẽ bên,trong đó ox//o,x',oy//o'y'.Chứng minh rằng xoy = x'o'y'
