a) 

Để : \(\frac{3.x+9}{x+4}\)là số nguyên thì : 

3.x + 9 \(⋮\)x + 4 

=> 3.x + 12 - 3 \(⋮\)x + 4 

=> 3 . ( x + 4 ) - 3\(⋮\)x + 4

=> -3 \(⋮\)x + 4 . Vì 3 . ( x + 4 ) \(⋮\)x + 4 

=> x + 4 \(\in\)Ư_{( -3 )} \(\in\){ -1; 1; -4; 4 }

=> x = { -5; -3; -9; -1 } để \(\frac{3.x+9}{x+4}\)là một số nguyên 

b)

Để : \(\frac{2.x-2}{2.x+3}\)là một số nguyên thì : 

2.x - 2 \(⋮\)2.x + 3 

2.x + 3 - 5 \(⋮\)2.x + 3

=> -5 \(⋮\)2.x + 3 . Vì 2.x + 3 \(⋮\)2.x + 3

=> 2.x + 3 \(\in\)Ư_{( -5 )} \(\in\){ -1; 1; -5; 5 } 

=> 2.x = { -4; -2; -8; 2 }

=> x = { -2; -1; -4; 1 } để \(\frac{2.x-2}{2.x+3}\)là một số nguyên

I. Nội qui tham gia "Giúp tôi giải toán"

1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;

2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.

3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp .

Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

tôi mong các bn sẽ ko làm như vậy !!!!!

MK ko biế đúng ko nữa , sai thì ý kiến

a)

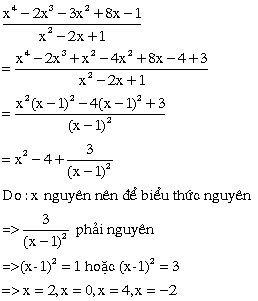
b)

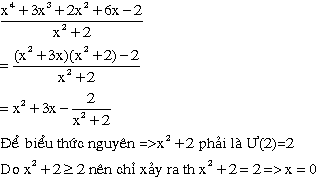
Chúc các bn hok tốt

Tham khảo nhé

\(C=\dfrac{\left(x^2+3x\right)\left(x^2+2\right)-2}{x^2+2}=x^2+3x-\dfrac{2}{x^2+2}\)

\(C\in Z\Leftrightarrow2⋮\left(x^2+2\right)\)

\(\Leftrightarrow x^2+2=2\Rightarrow x=0\)

\(C=\frac{6x-1}{3x+2}=\frac{6x+4-5}{3x+2}=2-\frac{5}{3x+2}\)là số nguyên \(\Leftrightarrow\frac{5}{3x+2}\)nguyên mà \(x\)nguyên nên 

\(3x+2\inƯ\left(5\right)=\left\{-5,-1,1,5\right\}\Leftrightarrow x\in\left\{-1,1\right\}\)(vì \(x\)nguyên) 

Thử lại thấy \(x=1\)thỏa mãn \(M=5x+11\)là số chính phương. 

Vậy giá trị của \(x\)thỏa mãn là \(1\).

ĐKXĐ: \(x\ne\pm3\)

a

Khi x = 1:

\(A=\dfrac{3.1+2}{1-3}=\dfrac{5}{-2}=-2,5\)

Khi x = 2:

\(A=\dfrac{3.2+2}{2-3}=-8\)

Khi x = \(\dfrac{5}{2}:\)

\(A=\dfrac{3.2,5+2}{2,5-3}=\dfrac{9,5}{-0,5}=-19\)

b

Để A nguyên => \(\dfrac{3x+2}{x-3}\) nguyên

\(\Leftrightarrow3x+2⋮\left(x-3\right)\\3\left(x-3\right)+11⋮\left(x-3\right) \)

Vì \(3\left(x-3\right)⋮\left(x-3\right)\) nên \(11⋮\left(x-3\right)\)

\(\Rightarrow\left(x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\\ \Rightarrow x\left\{4;2;-8;14\right\}\)

c

Để B nguyên => \(\dfrac{x^2+3x-7}{x+3}\) nguyên

\(\Rightarrow x\left(x+3\right)-7⋮\left(x+3\right)\)

\(\Rightarrow-7⋮\left(x+3\right)\\ \Rightarrow x+3\inƯ\left\{\pm1;\pm7\right\}\)

\(\Rightarrow x=\left\{-4;-11;-2;4\right\}\)

d

\(\left\{{}\begin{matrix}A.nguyên.\Leftrightarrow x=\left\{-8;2;4;14\right\}\\B.nguyên\Leftrightarrow x=\left\{-11;-4;-2;4\right\}\end{matrix}\right.\)

=> Để A, B cùng là số nguyên thì x = 4.

5. Ta có: a(a - 1) - (a + 3)(a + 2) = a² - a - a² - 2a - 3a - 6

           = -6a - 6 = -6(a + 1) \(⋮\)6

<=> -6(a + 1) \(⋮\)6 \(\forall\)a \(\in\)Z

<=> a(a - 1) - (a + 3)(a + 2) \(⋮\) 6 \(\forall\)a \(\in\)Z

6. Thay x = 99 vào biểu thức A, ta có:

A = 99⁵ - 100.99⁴ + 100. 99³ - 100.99² + 100 . 99 - 9

A = 99⁵ - (99 + 1).99⁴ + (99 + 1).99³ - (99 + 1).99² + (99 + 1).99 - 9

A = 99⁵ - 99⁵ - 99⁴ + 99⁴ + 99³ - 99³ - 99² + 99² + 99 - 9

A = 99 - 9 

A = 90

Vậy ....

Bài 3:

(3x-1)(2x+7)-(x+1)(6x-5)=16.

=> 6x²+21x-2x-7-(6x^2-5x+6x-5)=16

=>  6x²+21x-2x-7-6x²+5x-6x+5=16

=> 18x-2=16

=> 18x=16+2

=> 18x=18

=> x=1

Bài 4:

ta có : \(n\left(n+5\right)-\left(n-3\right)\left(n+2\right)=n^2+5n-\left(n^2+2n-3n-6\right)\)

\(=n^2+5n-n^2-2n+3n+6\)

\(=6n+6=6\left(n+1\right)⋮6\)

⇔6(n+1) chia hết cho 6 với mọi n là số nguyên

⇔n(n+5)−(n−3)(n+2) chia hết cho 6 với mọi n là số nguyên

vậy n(n+5)−(n−3)(n+2) chia hết cho 6 với mọi n là số nguyên (đpcm)

Bài 6:

\(A=x^5-100x^4+100x^3-100x^2+100x-9\)

\(\Rightarrow A=x^5-\left(99+1\right)x^4+\left(99+1\right)x^3-\left(99+1\right)x^2+\left(99+1\right)x-9\)

\(\Rightarrow A=x^5-99x^4-x^4+99x^3+x^3-99x^2-x^2+99x+x-9\)

\(\Rightarrow A=\left(x^5-99x^4\right)-\left(x^4-99x^3\right)+\left(x^3-99x^2\right)-\left(x^2-99x\right)+x-9\)

\(\Rightarrow A=x^4\left(x-99\right)-x^3\left(x-99\right)+x^2\left(x-99\right)-x\left(x-99\right)+x-9\)

\(\Rightarrow A=\left(x-99\right)\left(x^4-x^3+x^2-x\right)+x-9\)

Thay 99=x, ta được:

\(A=\left(x-x\right)\left(x^4-x^3+x^2-x\right)+x-9\)

\(\Rightarrow A=x-9\)

Thay x=99 ta được:

\(A=99-9=90\)

TL:

bài 4:

<=>n^2+5n-n^2-2n+3n+6

<=>6n+6

<=>6(n+1)

mà 6(n+1)\(⋮\) 6

=>n(n+5)-(n-3)(n+2)\(⋮\) 6(đpcm)

\(A=\frac{3x+9}{x-4}=\frac{x-4+2x+13}{x-4}=1+\frac{2x+13}{x-4}\)

\(A=1+\frac{x-4+x+9}{x-4}=1+1+\frac{x+9}{x-4}\)

\(A=2+\frac{x-4+13}{x-4}=2+1+\frac{13}{x-4}\)

\(A=3+\frac{13}{x-4}\)

Để A nguyên thì x - 4 thuộc Ư(13) = {+-1 ; +- 13}

x - 4                  1                      -1                                13                          -13

x                       5                        3                                17                           9

Vậy để A nguyên thì x thuộc {3 ; 5 ; 9 ; 17}

ĐKXĐ: x-4 khác 0 => x khác 4

\(\frac{3x+9}{x-4}=\frac{3x-12+21}{x-4}=\frac{3\left(x-4\right)+21}{x-4}=3+\frac{21}{x-4}\)

A nguyên => \(\frac{21}{x-4}\)nguyên

=> 21 chia hết cho x-4

=> x-4 thuộc Ư(21)={-21;;-7;-3;-1;1;3;7;21}

=> x thuộc (-17;-3;1;3;7;11;25)

Sau đó tính A ra nha b:)

\(A=\frac{3x+9}{x-4}=\frac{3\left(x-4\right)+21}{x-4}=\frac{3\left(x-4\right)}{x-4}+\frac{21}{x-4}=3+\frac{21}{x-4}\left(ĐK:x\ne4\right)\)

Để A nguyên \(\Rightarrow21⋮x-4\)hay \(x-4\inƯ\left(21\right)\)

Ta có : \(x-4\inƯ\left(21\right)\in\left\{\pm1;\pm3;\pm7;\pm21\right\}\)

Đến bước này bạn có thể lập bảng . Nhưng mình làm tắt nhé

\(\Rightarrow x\in\left\{5;3;7;1;11;-3;25;-17\right\}\)

Đặt x vào rồi sẽ tính được A