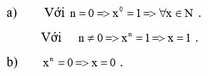Tìm x,y,z là số nguyên biết : xn + yn = zn với n là số tự nhiên khác 0.

Những câu hỏi liên quan
Tìm x,y,z là số nguyên biết : xn + yn = zn với n là số tự nhiên khác 0.
Tìm các số tự nhiên khác 0 là x, y, z biết xyz = 4(x + y + z).
Vì vai trò của x,y,z như nhau nên có thể giả sử \(x\ge y\ge z\)
Khi đó : \(xyz=4\left(x+y+z\right)\le12x\Rightarrow yz\le12\)
\(z^2\le12\Rightarrow z^2\in\left\{1;4;9\right\}\Rightarrow z\in\left\{1;2;3\right\}\)
+) Trường hợp 1 :
\(z=1\)thì \(xy=4\left(x+y+1\right)\Leftrightarrow\left(x-4\right)\left(y-4\right)=20\)
Nên \(x-4\)và \(y-4\) là ước của 20 với \(x-4\ge y-4\ge-3\) ( do \(x\ge y\ge z=1)\)
| x - 4 | 20 | 10 | 5 | 4 | 2 | 1 |
| y - 4 | 1 | 2 | 4 | 5 | 10 | 20 |
| x | 24 | 14 | 9 | 8 | 6 | 5 |
| y | 5 | 6 | 8 | 9 | 14 | 24 |
Vậy ta được cặp \(\left(x;y\right)\)là \(\left(24;5\right);\left(14;6\right);\left(9;8\right)\)
Xét tiếp trường hợp \(z=2;z=3\)
1. Tìm các số tự nhiên x, y, z nhỏ nhất khác 0 thoả mãn: 20x = 25y = 30z
2. Tìm tất cả các số nguyên n biết: (2n + 1)\(⋮\)(n-1).
Bài 1:
Đặt $20x=25y=30z=t$ với $t$ là số tự nhiên khác 0.
$\Rightarrow x=\frac{t}{20}; y=\frac{t}{25}; z=\frac{t}{30}$
Để $x,y,z$ là stn thì $t\vdots 20,25,30$
$\Rightarrow t=BC(20,25,30)$
Để $x,y,z$ nhỏ nhất và khác 0 thì $t$ nhỏ nhất và khác 0
$\Rightarrow t=BCNN(20,25,30)$ sao cho $t\neq 0$
$\Rightarrow t=300$
$\Rightarrow x=\frac{t}{20}=\frac{300}{20}=15, y=\frac{t}{25}=\frac{300}{25}=12; z=\frac{300}{30}=10$
Đúng 1
Bình luận (0)
Bài 2:
$2n+1\vdots n-1$
$\Rightarrow 2(n-1)+3\vdots n-1$
$\Rightarrow 3\vdots n-1$
$\Rightarrow n-1\in \left\{1; -1; 3;-3\right\}$
$\Rightarrow n\in \left\{3; 0; 4; -2\right\}$
Đúng 0
Bình luận (0)
a) Tìm số tự nhiên x và y biết y là số nguyên tố và x . y = 28
b) Tìm số tự nhiên x biết x khác 0 và x là số bé nhất trong các số chia hết cho 36 và 90
a: Vì y là số nguyên tố
mà y là ước của 28
nên y=2
=>x=14
b: Theo đề, ta có: x=BCNN(36;90)
hay x=180
Đúng 1
Bình luận (0)
a) Tìm số tự nhiên x và y biết y là số nguyên tố và x . y = 28
b) Tìm số tự nhiên x biết x khác 0 và x là số bé nhất trong các số chia hết cho 36 và 90
bài kia quá dễ cậu ko làm đc thì học lớp 6 làm gì![]()
Đúng 1
Bình luận (0)
1. Cho x(m+n)=y(n+p)=z(p+m) trong đó x, y, z là các số khác nhau và khác 0, chứng minh rằng: (m-n)/x(y-z)=(n-p)/y(z-x)=(p-m)/z(x-y)
2. Số tự nhiên A = 1+ 2^3^2012 là số nguyên tố hay hợp số?Giải thích?
Chứng minh rằng x-y là ước của xm+yn thì x-y cũng là ước của xn+ym(Với x,y,m,n là số nguyên)
Tìm số tự nhiên x, biết rằng với mọi n ∈ N ta có:
a) x n = 1
b) x n = 0
Tìm số tự nhiên x, biết rằng với mọi n ∈ N ta có:
a, x n = 1
b, x n = 0
a, Với n = 0 => x 0 = 1 ⇒ ∀ x ∈ N
Với n ≠ 0 => x n = 1 ⇒ x = 1
b, x n = 0 => x = 0
Đúng 0
Bình luận (0)