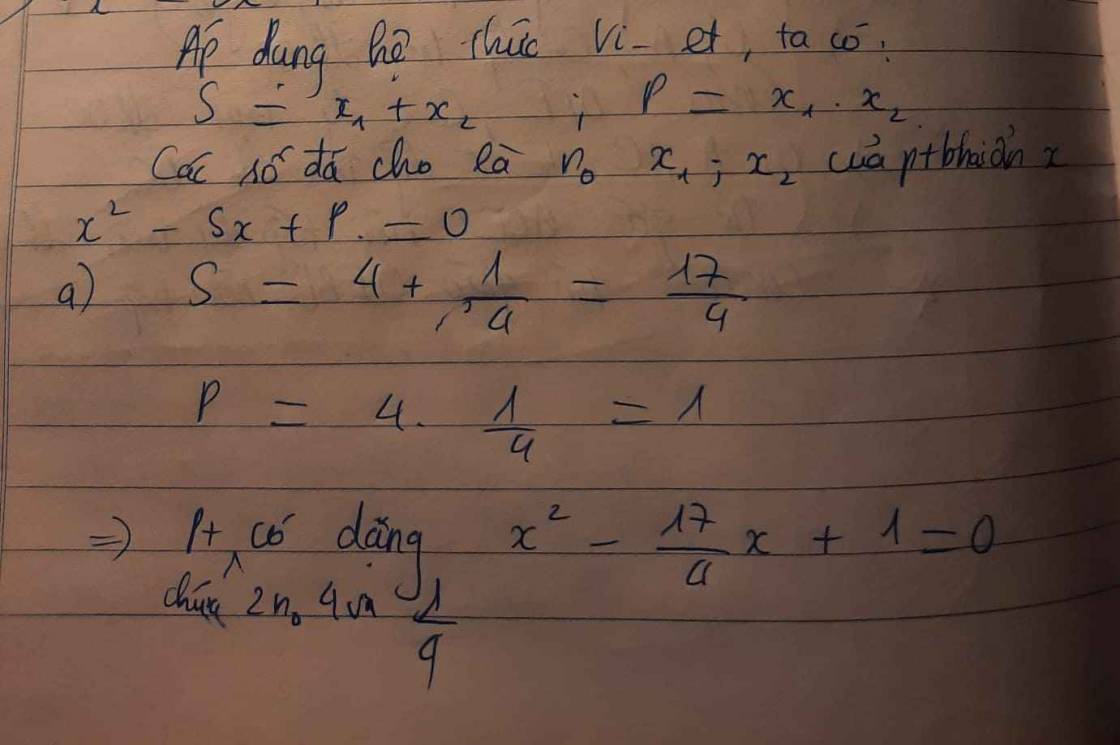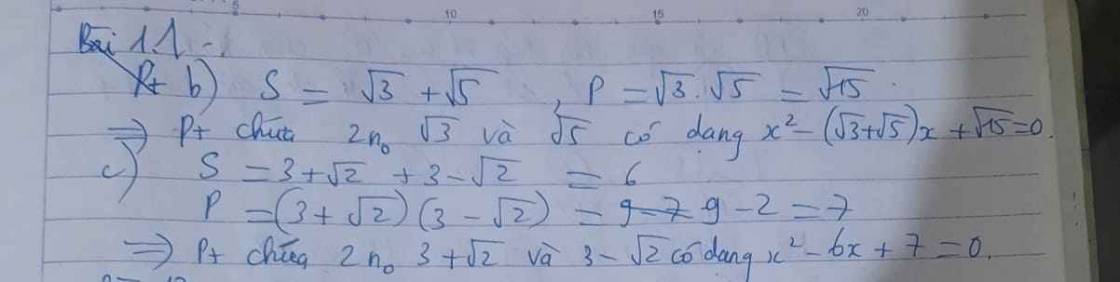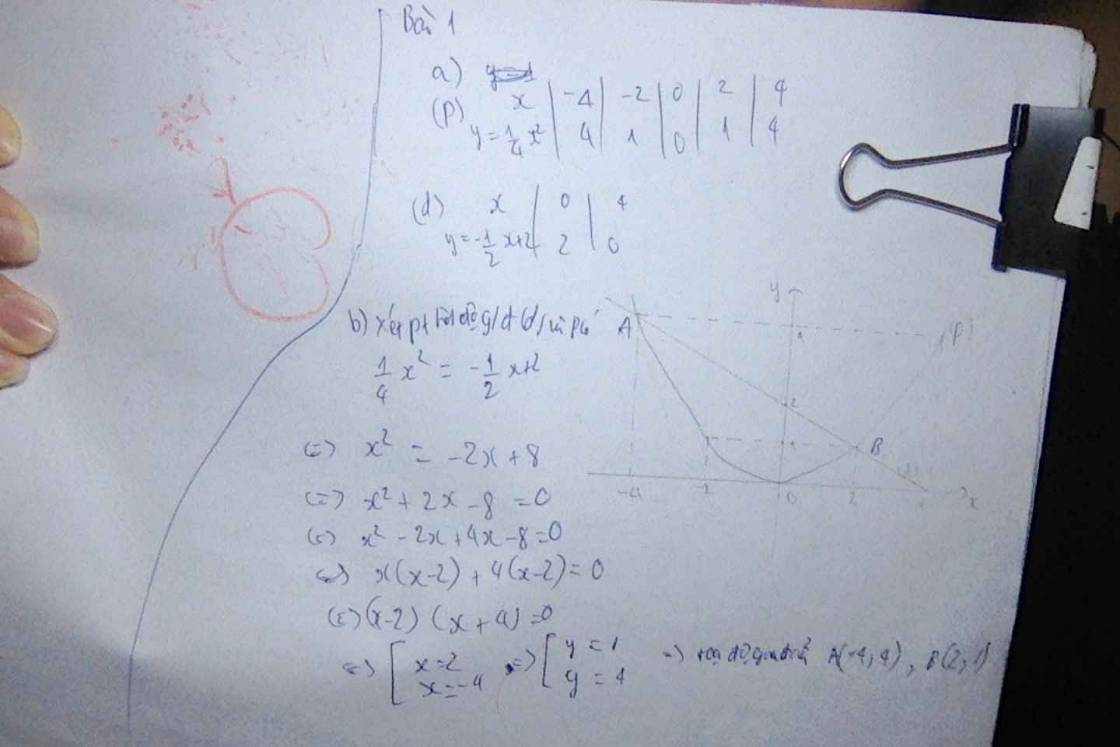\(\dfrac12 + \dfrac14\)

Những câu hỏi liên quan
\(\dfrac56 x (\dfrac12 + \dfrac12) \)
\(\dfrac{5}{6}\times\left(\dfrac{1}{2}+\dfrac{1}{2}\right)=\dfrac{5}{6}\times\dfrac{2}{2}=\dfrac{5}{6}\times1=\dfrac{5}{6}\)
Đúng 4
Bình luận (6)
Xem thêm câu trả lời
\(quy đồng : \dfrac56 và \dfrac14\)
\(\dfrac{5}{6}=\dfrac{10}{12};\dfrac{1}{4}=\dfrac{3}{12}\)
Đúng 1
Bình luận (0)
\(\dfrac{5}{6}=\dfrac{20}{24};\dfrac{1}{4}=\dfrac{6}{24}\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
\(\dfrac3{10} + x = \dfrac12\)
Xem thêm câu trả lời
dfrac23 + (dfrac34 + dfrac12 ) (...+dfrac34)
Đọc tiếp
\(\dfrac23 +\) (\(\dfrac34 + \dfrac12\) ) = (\(...+\dfrac34\))
Lập phương trình bậc hai có các nghiệm:
a) $4$ và $\dfrac14$;
b) $\sqrt{3}$ và $\sqrt{5}$;
c) $3+\sqrt{2}$ và $3-\sqrt{2}$.
a) x2 -\(\dfrac{17}{4}x+1=0\)
b) x2-(\(\sqrt{3}+\sqrt{5}\))x+\(\sqrt{15}=0\)
c)x2-6x+7=0
Xem thêm câu trả lời
Cho parabol $(P)$: $y = \dfrac14 x^2$ và đường thẳng $(d):$ $y = -\dfrac12x + 2$.
a. Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.
b. Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
b,
Phương trình hoàng độ giao điểm của (p) và (d) là:
1
4
x
2
=
−
1
2
x
+
2
⇔
1
4
x
2
+
1
2
x
−
2
=
0
⇔
x
2
+
2
x
−
8
=
0
⇔
(
x
+
4
)
(
x
−
2
)
=
0
⇔
\orbr
{
x
=
−
4
x
=
2
x
=
−
4
⇒
y
=
4
x
=
2
⇒
y
=
1
Vậy tọa độ giao điểm của (p) và (d) là (-4;4) ; (2;1)
vậy tọa độ (P) và (d) là A (2;1) và B(-4;4)
Cho tập hợp $X = \{1; \, \sqrt2; \, \sqrt3; \, ...; \, \sqrt{2024}\}$. Chứng minh rằng trong $90$ số khác nhau bất kì được lấy ra từ tập $X$ luôn tồn tại hai số $x$, $y$ sao cho $|x - y| < \dfrac12$.
Câu 12. Khoanh vào:
a) $dfrac16$ số ngôi sao có trong hình sau.
b) $dfrac12$ số quả lê có trong hình sau.
Đọc tiếp
Câu 12. Khoanh vào:
a) $\dfrac16$ số ngôi sao có trong hình sau.

b) $\dfrac12$ số quả lê có trong hình sau.

1 phần 6 số ngôi sao là 3.
1 phần 2 số quả lê là 3.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho ΔABC (AB = BC). Trên tia đối của tia CB lấy điểm D sao cho CD = AB. Trên tia đối của tia BA lấy BE = BH (H là trung điểm BC). Đường thẳng AE cắt AD tại F. Chứng minh:
a) ∠ADB = \(\dfrac12\) BC
b) FA = AD
c) FA = FH = FD
d) Tính ∠AFH; ∠ADB. Biết ∠BAC = 58o
GIÚP MÌNH VỚI Ạ! Mình đang cần T.T Cảm ơn ạ!