Cho tam giác ABC vuông tại A đường cao AH . Gọi D sao cho AB là trung trực của HD.Lấy điểm E sao cho AC là trung trực của HE. Chứng minh A,D,E thẳng hàng
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Lấy điểm D sao cho AB là trung trực của HD, AB cắt HD tại P. Lấy điểm E sao cho AC là trung trực của HE, AC cắt HE tại Q. Chứng minh:
a) Ba điểm A,D,E thẳng hàng
b) PQ // DE
a) Xét tứ giác APHQ: ^PAQ=^APH=^AQH=900 => Tứ giác APHQ là hình chữ nhật
=> AP=HQ. Mà HQ=EQ => AP=EQ.
Ta có: AP vuông góc AC; EQ vuông góc AC => AP // EQ (Quan hệ song song vuông góc)
Xét tứ giác APQE: AP=EQ; AP // EQ => Tứ giác APQE là hình bình hành => PQ // AE (1)
Tương tự: Tứ giác AQPD là hình bình hành => PQ // AD (2)
Từ (1) và (2) => 2 điểm D;A;E thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).
b) Ta thấy điểm A thuộc DE, PQ // AD và PQ//AE nên PQ // DE (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A . Kẻ đường cao AH . Trên tia Hx vuông góc với AB , lấy điểm D sao cho AB là đường trung trực của đt HD . Trên tia Hy vuông góc với AC lấy điểm E sao cho AC là đường trung trực của HE
a) CM ba điểm D,E,A thẳng hàng
b ) CM tứ giác BCDE là hình thang vuông
a: Ta có: H và D đối xứng với nhau qua AB
nên AH=AD; BH=BD
=>ΔHAD cân tại A
=>AB là phân giác của góc HAD(1)
Ta có H và E đối xứngvới nhau qua AC
nên AH=AE; CH=CE
=>ΔAHE cân tại A
=>AC là phân giác của góc HAE(2)
Từ (1) và (2) suy ra góc DAE=2xgóc BAC=180 độ
=>D,A,E thẳng hàng
b: Xét ΔAHB và ΔADB có
AH=AD
BH=BD
AB chung
Do đó: ΔAHB=ΔADB
Suy ra: góc ADB=90 độ
=>BD vuông góc với DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
HC=EC
AC chung
Do đó: ΔAHC=ΔAEC
Suy ra: góc AEC=90 độ
=>CE vuông góc với ED(4)
Từ (3) và (4) suy ra BDEC là hình thang vuông
c: ED=AE+AD
=AH+AH=2AH
d: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
Do đó: ΔDHE vuông tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, ba đường cao AH,BM,CN. Lấy D sao cho AB là đường trung trực của HD, lấy E sao cho AC là đường trung trực của HE. Kẻ AP vuông góc với MN. Chứng minh rằng:
a) tam giác ADE cân tại A
b) Ha là tia phân giác của góc MHN
c) 4 điểm M,N,D,E thẳng hàng
d) góc BAH= góc PAC.
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia Hx vuông góc với AB lấy điểm D sao cho AB là đường trung trực của HD. Trên tia Hy vuông góc với AC lấy điểm E sao cho AC là đường trung trựcHE.
a) Chứng minh 3 điểm D,A,E thẳng hàng
b) Chứng minh tứ giác BCED là hình thang vuông
c) Chứng minh ED=2AH
d) Chứng minh tam giác DHE vuông
Xem thêm câu trả lời
Cho tam giác ABC, đường cao AH. Vẽ điểm D sao cho AB là đường trung trực của HD. Vẽ điểm E sao cho AC là đường trung trực của HE. Gọi M, N theo thứ tự là giao điểm của DE với AB, AC. Xét xem các đường thẳng sau là các đường gì trong tam giác HMN: MB, NC, HA, HC, MC, từ đó hãy chứng minh rằng MC vuông góc với AB.
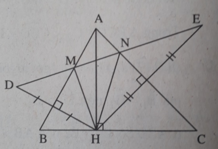
M thuộc đường trung trực của HD nên MH = MD. MB là đường trung trực của đáy HD của tam giác cân HMD nên MB là tia phân giác của góc HMD. Tương tự NC là tia phân giác của góc HNE. Vậy MB, NC là các đường phân giác góc ngoài của ΔHMN.
Các đường thẳng MB, NC cắt nhau tại A nên HA là đường phân giác trong của góc MHN của ΔHMN.
+) HC vuông góc với HA tại H mà HA là đường phân giác trong của góc MHN nên HC là đường phân giác góc ngoài của ΔHMN.( đường phân giác góc trong và góc ngoài tại 1 đỉnh của 1 tam giác vuông góc với nhau)
+) Các đường thẳng HC và NC cắt nhau tại C; HC và NC là hai đường phân giác ngoài của tam giác HMN nên MC là đường phân giác góc trong của ΔHMN.
MB và MC là các tia phân giác của hai góc kề bù ∠DMH; ∠HMA nên MB ⊥ MC.
Vậy MC ⊥ AB.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Đường cao AH. Trên tia Hx vuông góc với AB, ta lấy điểm D sao cho AB là đường trung trực của HD. Trên tia HI vuông góc với AC ta cũng lấy điểm E sao cho AC là trung trực của đoạn thẳng HE. CMR:
a, Ba điểm D,A,E thẳng hàng.
b, Tứ giác BCED là hình thang vuông.
c, DE=2AH
d,Tam giác DHE là tam giác vuông.
Giúp mik nhanh nha.
Gấp gáp chi em cuộc sống vẫn rực rỡ sắc màu
Chim vẫn reo ca và môi hôn đang đứng đợi
Hoa vẫn nở và xuân thì đương tới
Hãy trải lòng xao xuyến với tình yêu.
Đúng 0
Bình luận (0)
a: Ta có: H và D đối xứng với nhau qua AB
nên AH=AD; BH=BD
=>ΔHAD cân tại A
=>AB là phân giác của góc HAD(1)
Ta có H và E đối xứngvới nhau qua AC
nên AH=AE; CH=CE
=>ΔAHE cân tại A
=>AC là phân giác của góc HAE(2)
Từ (1) và (2) suy ra góc DAE=2xgóc BAC=180 độ
=>D,A,E thẳng hàng
b: Xét ΔAHB và ΔADB có
AH=AD
BH=BD
AB chung
Do đó: ΔAHB=ΔADB
Suy ra: góc ADB=90 độ
=>BD vuông góc với DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
HC=EC
AC chung
Do đó: ΔAHC=ΔAEC
Suy ra: góc AEC=90 độ
=>CE vuông góc với ED(4)
Từ (3) và (4) suy ra BDEC là hình thang vuông
c: ED=AE+AD
=AH+AH=2AH
d: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
Do đó: ΔDHE vuông tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Lấy điểm D trên cạnh BC Sao cho BD=BA. Chứng minh AD là phân giác của góc CAH. Gọi E là hình chiếu của D trên AC.
Chứng minh AD là đường trung trực của đoạn thẳng HE theo nhiều cách.
Chứng minh BC+AH>AB+AC
a)Cm: AD là phân giác của góc CAH.
Xét Tam giác BAD cân tại B (Vì BD=BA).
Kẽ BI là phân giác của góc B.( đồng thời là đường cao)
=> Góc ABI= Góc IBD (1)
Xét Tam giác IBD vng tại I có:
Góc IBD+Góc ADB=900 (2)
Ta lại xét tam giác AHD vng tại D có:
Góc HAD+Góc ADH=900 (3)
Từ (1),(2) và (3) ta suy ra Góc IBD=Góc HAD=1/2 góc B
Mà ta lại có góc B= góc HAC( cùng phụ với C)
=>HAD=1/2HAC
=>AD là phân giác của góc CAH (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB AC 10cm, BC 12cm. Kẻ AH vuông góc với BC tại Ha) Chứng minh rằng H làtrung điểm của đoaṇ thẳng BCb) Tính độ dài đoạn thẳng AHc) Kẻ HI AB taị I và HK AC taị K. Vẽ các điểm D và E sao cho I ,K lần lươṭ làtrung điểmcủa HD và HE. Chứng minh AE AH . Tam giác ADE là tam giác gì? Vì sao?d) Chứng minh AH là đường trung trực của đoạn thẳng DE .e) Tìm điều kiện của tam giác ABC để A là trung điểm của DECho tam giác ABC có AB AC 10cm, BC 12cm. Kẻ AH vuông góc với BC tại Ha...
Đọc tiếp
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh rằng H là
trung điểm của đoaṇ thẳng BC
b) Tính độ dài đoạn thẳng AH
c) Kẻ HI AB taị I và HK AC taị K. Vẽ các điểm D và E sao cho I ,K lần lươṭ là
trung điểm
của HD và HE. Chứng minh AE = AH . Tam giác ADE là tam giác gì? Vì sao?
d) Chứng minh AH là đường trung trực của đoạn thẳng DE .
e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh rằng H là
trung điểm của đoaṇ thẳng BC
b) Tính độ dài đoạn thẳng AH
c) Kẻ HI AB taị I và HK AC taị K. Vẽ các điểm D và E sao cho I ,K lần lươṭ là
trung điểm
của HD và HE. Chứng minh AE = AH . Tam giác ADE là tam giác gì? Vì sao?
d) Chứng minh AH là đường trung trực của đoạn thẳng DE .
e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE
Cho tam giác ABC vuông cân tại A, đường cao AH. Lấy điểm D sao cho AB là trung trực của DH. Lấy E sao cho AC là trung trực của HE. CMR: DE= 2AH