Chứng minh định lí:
Hai tia phân giác của hai góc kề bù thì tạo thành góc vuông
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
Hãy vẽ hai góc xOy và yOx’ kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot’ của góc yOx’ và gọi số đo của góc xOy là mº.
Chứng minh rằng: Hai tia phân giác của 2 góc kề bù tạo thành 1 góc vuông
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
hình tự vẽ nha
Hãy chứng minh hai tia phân giác của 2 góc kề bù tạo thành góc vuông
Góc xOy + yOz = 180
Có O1 = O2 (Om phân giác) O3 = O4 (On phân giác)
mà O1 + O2 +O3 + O4 = 180 <=> 2.O2+ 2.O3 = 180 <=> O2+O3 = 90 hay góc mOn = 90 => đpcm
Cho định lí: Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông
-Chứng minh định lí trên
Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
\(\Rightarrow\begin{cases}\widehat{O_1}=\widehat{O_2}=\frac{1}{2}.\widehat{xOy}\\\widehat{O_3}=\widehat{O_4}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{O_2}+\widehat{O_3}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180^0=90^0\)
=> Đpcm
* Vẽ hình: Vẽ hình hơi xấu chút! ![]()
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
Chứng minh :
\(\widehat{mOz=\frac{1}{2}}\widehat{xOz}\) \(\left(1\right)\) ( vì Om là hai tia phân giác của \(\widehat{xOz}\) )
\(\widehat{zOn}=\frac{1}{2}\widehat{zOy}\) \(\left(2\right)\) ( vì On là hai tia phân giác của \(\widehat{zOy}\) )
Từ \(\left(1\right)\) và \(\left(2\right)\) , ta có :
\(\widehat{mOz}+\widehat{zOn}=\frac{1}{2}.\left(\widehat{xOz}+\widehat{zOy}\right)\) \(\left(3\right)\)
Vì tia \(Oz\) nằm giữa hai tia \(Om,On\) và vì \(\widehat{xOz}\) và \(\widehat{zOy}\) kề bù \(\left(gt\right)\)
Nên từ \(\left(3\right)\) \(\Rightarrow\widehat{mOn}=\frac{1}{2}.180^0\)
Hay \(\widehat{mOn}=90^0\)
chứng minh định lí Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
Hãy viết giả thiết và kết luận của định lí
Chứng minh định lí sau: Hai tia phân giác của một cặp góc kề bù thì vuông góc với nhau
Tham khảo nhé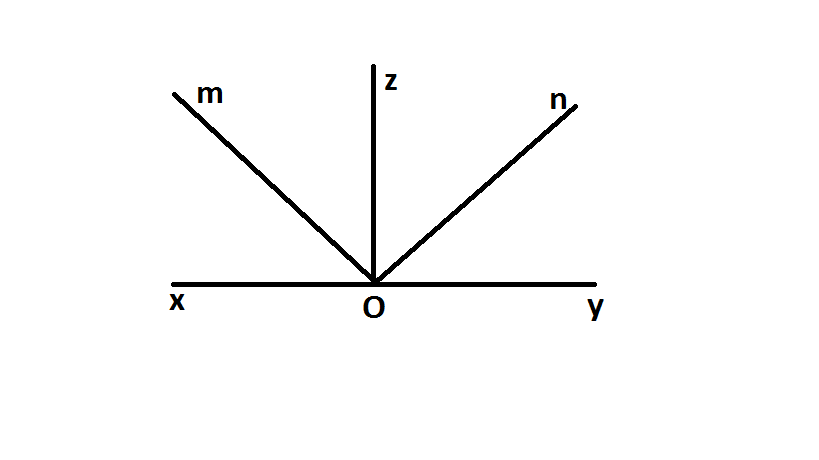
Ta có góc \(\widehat{\text{xOz}}\) + \(\widehat{\text{zOy}}\) = 180\(^o\)(kề bù)
=> 2(\(\widehat{mOz}\) +\(\widehat{zOn}\)) = 180\(^o\)
=> \(\widehat{mOz}\) + \(\widehat{zOn}\) = 90\(^o\)
=>\(\widehat{mOn}\) = 90\(^o\) (vì \(\widehat{xOz}\), \(\widehat{xOz}\) kề nhau)
=> Tia Om vuông góc tia On
Vậy 2 tia phân giác của 1 cặp góc kề bù thì vuông góc với nhau
2 : Phát biểu tính chất : " Hai tia phân giác của 2 góc kề bù tạo thành góc vuông " thành định lí dạng : Nếu.... thì
rồi vẽ hình và ghi Giả thiết , kết luận của định lí
Chứng minh định lí và phát biểu
Nếu Ox,Oy là hai tia phân giác của hai góc kề bù thì Ox\(\perp Oy\)
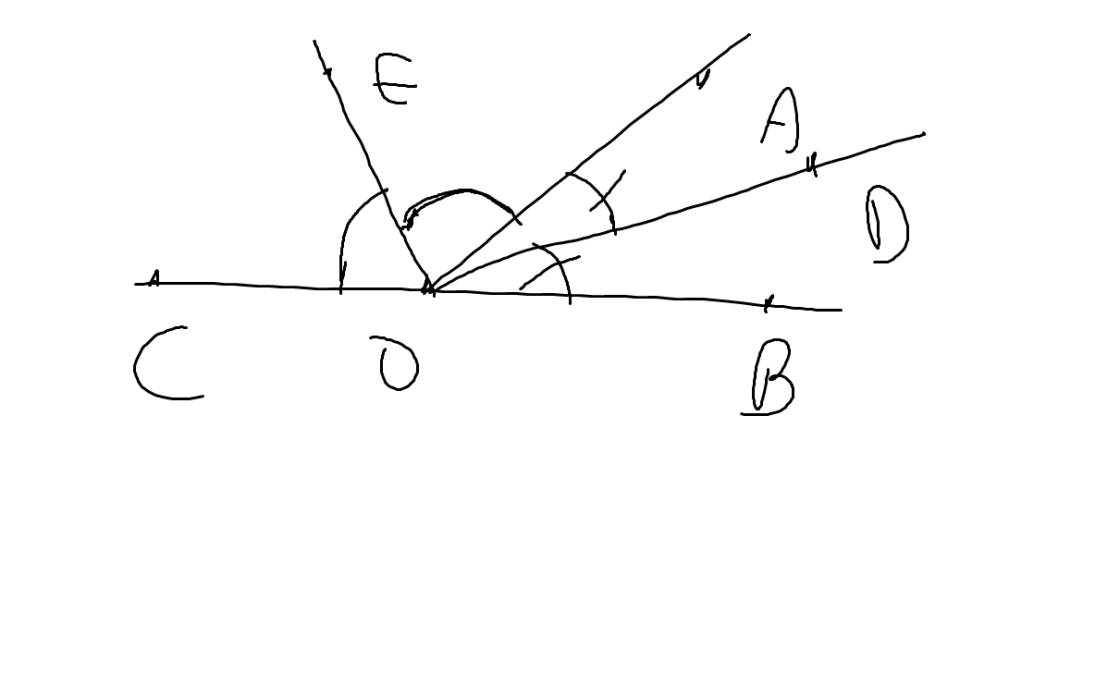
| GT | \(\widehat{AOB};\widehat{AOC}\) là hai góc kề bù OD,OE lần lượt là phân giác của \(\widehat{AOB};\widehat{AOC}\) |
| KL | OD\(\perp\)OE |
OD là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOB}=2\cdot\widehat{AOD}\)
OE là phân giác của \(\widehat{AOC}\)
=>\(\widehat{AOC}=2\cdot\widehat{AOE}\)
\(\widehat{AOB}+\widehat{AOC}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOE}+2\cdot\widehat{AOD}=180^0\)
=>\(\widehat{AOE}+\widehat{AOD}=90^0\)
=>\(\widehat{EOD}=90^0\)
=>OE\(\perp\)OD(ĐPCM)
Chứng minh rằng góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.