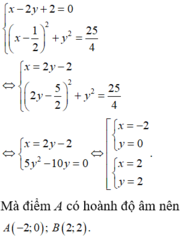Cho hình chữ nhật ABCD. Đường AB có pt:y-2=0 Điểm E thuộc cạnh AB sao cho AB=4AE. Biết phương trình DE:2x-y+3=0 diện tích tam giác CDE bằng 9. Tìm tọa độ các đỉnh hình chữ nhật, biết D có hoành độ âm.

Những câu hỏi liên quan
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có AB = 3BC, M(3/2; -3/2) là trung điểm của AD, N là điểm trên cạnh AB thỏa BN = 2AN. Tìm tọa độ các đỉnh của hình chữ nhật ABCD biết phương trình đường AN: x - 3y - 2 = 0 và điểm C có hoành độ dương.
AN chính là đường thẳng AB nên AB: x-2y-2=0.
AD qua M(3/2;-3/2) và vuông góc với AB nên AD: 2x+y-3/2=0. Suy ra A(1;-1/2)
Vì M là trung điểm AD nên D(2;-5/2) suy ra BC=AD=\(\sqrt{5}\), suy ra AB=3BC=3\(\sqrt{5}\)
B(2b+2;b) nên
\(AB=\sqrt{(2b+1)^2+(b+1/2)^2}=\dfrac{\sqrt{5}}{2}|2b+1|=3\sqrt{5}\Rightarrow b=\dfrac{5}{2}\) hoặc \(b=-\dfrac{7}{2}\)
Nếu \(b=\dfrac{5}{2}\) thì B(7;5/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(8;-1/2) (thỏa mãn)
Nếu \(b=-\dfrac{7}{2}\) thì B(-5;-7/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(-4;-11/2) (loại)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có AB = 3BC, M(3/2; -3/2) là trung điểm của AD, N là điểm trên cạnh AB thỏa BN = 2AN. Tìm tọa độ các đỉnh của hình chữ nhật ABCD biết phương trình đường CN: x - 3y - 2 = 0 và điểm C có hoành độ dương.
Đặt BC=a, suy ra AB=3a.
$S_{MNC}=S_{ABCD}-S_{AMN}-S_{BNC}-S_{DMC}=3a^2-\dfrac{a^2}{4}-a^2-\dfrac{3a^2}{4}=a^2$
$CN=a\sqrt{5}$ nên $d(M,CN)=\dfrac{2S_{MNC}}{CN}=\dfrac{2a}{\sqrt{5}}$
Mặt khác $d(M,CN)=\dfrac{4}{\sqrt{10}}$ nên $a=\sqrt{2}$
Suy ra $MC=\dfrac{a\sqrt{37}a}{2}=\dfrac{\sqrt{74}}{2}$
Gọi C(3c+2;c) (3c+2>0) thì
$MC^2=(3c+1/2)^2+(c+3/2)^2=\dfrac{74}{4}\Leftrightarrow (6c+1)^2+(2c+3)^2=74$
$40c^2+24c-64=0$ nên c=1 hoặc c=-8/5(loại) nên C(5;1)
+ Tương tự tìm được N từ việc N thuộc CN, $MN=\dfrac{a\sqrt{5}}{2},CN=a\sqrt{5}$
+ Sau khi tìm được N ta tìm được E từ việc M là trung điểm CE
+ Tọa độ A, B xác định qua hệ thức véc tơ: vecto(EA)=3.vecto(AN); vecto(AN)=2vecto(NB)
+ Tọa độ D xác định từ việc M là trung điểm AD.
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có tâm \(I\left(\frac{1}{2};0\right)\) đường thẳng chứa cạnh AB có phương trình : \(x-2y+2=0\) và \(AB=2AD\).
Tìm tọa độ các đỉnh của hình chữ nhật, biết rằng đỉnh A có hoành độ âm.
\(d\left(I;AB\right)=\frac{\left|\frac{1}{2}+2\right|}{\sqrt{1^2+\left(-2\right)^2}}=\frac{\sqrt{5}}{2}\Rightarrow AD=2d\left(I;AB\right)=\sqrt{5}\)và \(AB=2AD=2\sqrt{5}\)
Do đó \(IA=IB=IC=ID=\frac{1}{2}AC=\frac{5}{2}\)
Gọi \(\omega\) là đường tròn tâm I, bán kính \(R=IA\) thế thì \(\omega\) có phương trình \(\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\)
Do vậy tọa độ của A, B là nghiệm của hệ :
\(\begin{cases}\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\\x-2y+2=0\end{cases}\)
Giải hệ thu được \(A\left(-2;0\right);B\left(2;2\right)\) (do A có hoành độ âm), từ đó , do I là trung điểm của AC và BD suy ra \(C\left(3;0\right);D\left(-1;-2\right)\)
Đúng 0
Bình luận (0)
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm
I
1
2
;
0
phương trình đường thẳng AB là x-2y+20 và AB2AD Tìm tọa độ điểm B, biết rằng điểm A có hoành độ âm A. B(-2;0) B. (2;2) C. B(3;0) D. (-1;-2)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm I 1 2 ; 0 phương trình đường thẳng AB là x-2y+2=0 và AB=2AD Tìm tọa độ điểm B, biết rằng điểm A có hoành độ âm
A. B(-2;0)
B. (2;2)
C. B(3;0)
D. (-1;-2)
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm \(I\left(\dfrac{1}{2};0\right)\) phương trình đường thẳng AB là : \(x-2y+2=0\) và AB = 2AD. Tìm tọa độ các đỉnh A, B, C, D biết đỉnh A có hoành độ âm ?
Cho hình chữ nhật ABCD có 2 điểm E,F lần lượt nằm trên các cạnh AB, AD sao cho EB=2EA, FA=3FD. Biết F(2;1), ptđt CE: x-3y-9=0, tam giác CEF vuông tại F. Tìm tọa độ điểm C biết C có hoành độ dương.
\(EF^2=AF^2+AE^2=\dfrac{9}{16}AD^2+\dfrac{1}{9}AB^2\)
\(CF^2=DF^2+CD^2=\dfrac{1}{16}AD^2+AB^2\)
\(CE^2=BC^2+EB^2=AD^2+\dfrac{4}{9}AB^2\)
Theo Pitago: \(EF^2+CF^2=CE^2\Rightarrow16AB^2=9AD^2\Rightarrow AD=\dfrac{4}{3}AB\)
\(\Rightarrow\left\{{}\begin{matrix}EF^2=\dfrac{10}{9}AB^2\\CF^2=\dfrac{10}{9}AB^2\end{matrix}\right.\) \(\Rightarrow EF=CF\)
Gọi H là hình chiếu vuông góc của F lên CE \(\Rightarrow H\) là trung điểm CE
Phương trình HF: \(3\left(x-2\right)+1\left(y-1\right)=0\Leftrightarrow3x+y-7=0\)
Tọa độ H là nghiệm: \(\left\{{}\begin{matrix}x-3y-9=0\\3x+y-7=0\end{matrix}\right.\) \(\Rightarrow H\left(3;-2\right)\)
Gọi \(C\left(3c+9;c\right)\Rightarrow E\left(-3c-3;-c-4\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{EF}=\left(3c+5;c+5\right)\\\overrightarrow{FC}=\left(3c+7;c-1\right)\end{matrix}\right.\)
\(EF\perp CF\Rightarrow\left(3c+5\right)\left(3c+7\right)+\left(c+5\right)\left(c-1\right)=0\)
\(\Leftrightarrow c^2+4c+3=0\Rightarrow\left[{}\begin{matrix}c=-1\Rightarrow C\left(6;-1\right)\\c=-3\Rightarrow C\left(0;-3\right)\left(loại\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD , đường thẳng BC có phương trình x+y-4=0, điểm M(-1,-1) là trung điểm của đoạn AD . Xác định tọa độ các đỉnh hình chữ nhật ABCD , biết đường thẳng AB đi qua điểm e(-1,1)
AB đi qua E và vuông góc BC nên nhận (1;-1) là 1 vtpt
Phương trình AB:
\(1\left(x+1\right)-1\left(y-1\right)=0\Leftrightarrow x-y+2=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(-3;-1\right)\)
Đường thẳng d qua M và song song AB có pt:
\(1\left(x+1\right)-1\left(y+1\right)=0\Leftrightarrow x-y=0\)
Gọi N là giao điểm d và BC \(\Rightarrow N\) là trung điểm BC
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x-y=0\\x+y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;2\right)\Rightarrow C\left(7;5\right)\)
Đường thẳng AD qua M và song song BC có pt:
\(1\left(x+1\right)+1\left(y+1\right)=0\Leftrightarrow x+y+2=0\)
A là giao điểm AB và AD nên tọa độ là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+2=0\end{matrix}\right.\) \(\Rightarrow A\left(-2;0\right)\)
\(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\) tọa độ D
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD Có AB: x-3y+7=0 AC : x+y-1=0. E thuộc đoạn AC sao cho AE =4EC .Bán kính đường tròn ngoại tiếp tam giác ADE là căn 10 .. B có hoành độ dương .Tìm tạo độ các đỉnh hình chữ nhật.