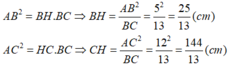Cho tam giác ABC vuông ở A và có đường cao AH,AB=5cm, AC=12cm
Tính độ dài các đoạn thẳng BC,AH
1) Cho tam giác ABC vuông ở A và có đường cao AH,AB=5cm, AC=12cm
Tính độ dài các đoạn thẳng BC,AH
2)Cho tam giác ABC( góc A=90 độ), đường cao AH. chứng minh rằng AH2=BH.CH
Cho tam giác ABC vuông tại A, đường cao AH
a, Cho biết AB = 3cm, BC = 5cm. Tính độ dài đoạn thẳng BH,CH, AH và AC
b, Cho biết AH = 60cm, CH = 144cm. Tính độ dài đoạn thẳng AB, AC, BC, và BH
a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
Cho hình bên là tam giác ABC vuông tại A, đường cao AH. Cho biết AB = 5cm, AC = 12cm. Tinh độ dài các đoạn thẳng BC, AH, BH và CH.
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta có:
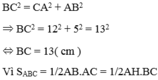
⇒ AH.BC = AB.AC
Hay 12.5 = AH.13 ⇒ AH = 60/13 ( cm )
Từ câu a ta có: Δ BHA ∼ Δ BAC ⇒ BH/BA = BA/BC hay BH/5 = 5/13 ⇔ BH = 25/13( cm )
Do đó: CH = BC - BH = 13 - 25/13 = 144/13( cm )
Cho tam giác ABC vuông tại A , đường cao AH
a, Cho biết AB = 3cm ,BC=5cm . Tính độ dài các đoạn thẳng BH, CH , AH và AC
b, Cho biết AH bằng 16 cm , BH=25cm . Tính độ dài các đoạn thẳng AB, AC , BC và CH
12AB.AC" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
12AH.BC" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
12AB.AC=12AH.BC" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
AB.ACBC=3.45=2,4(cm)" role="presentation" style="border:0px; box-sizing:inherit; direction:ltr; display:inline-block; float:none; font-size:18.08px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB =
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC =
cho tam giác vuông tại A,đường cao AH
a,cho biết AB = 3cm,BC = 5cm. Tính độ dài các đoạn thẳng BH,CH,AH và AC
b,cho biết AH = 60cm,CH = 144cm. Tính độ dài các đoạn thẳng AB,AC,BC và BH
c,cho biết AC = 12cm,AH = \(\dfrac{60}{13}cm.\) Tính độ dài các đoạn thẳng AB,BC<BH và CH
a: AC=căn 5^2-3^2=4cm
AH=3*4/5=2,4cm
BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
b: \(BH=\sqrt{60^2:144}=5\left(cm\right)\)
BC=144+5=149cm
\(AB=\sqrt{5\cdot149}=\sqrt{745}\left(cm\right)\)
\(AC=\sqrt{144\cdot149}=12\sqrt{149}\left(cm\right)\)
c: \(HC=\sqrt{AC^2-AH^2}=\dfrac{144}{13}\left(cm\right)\)
\(BH=\dfrac{AH^2}{HC}=\dfrac{25}{13}cm\)
BC=BH+CH=13(cm)
AB=căn 13^2-12^2=5cm
a
Áo dụng đl pytago vào tam giác ABC vuông tại A:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
\(CH=BC-BH=5-1,8=3,2\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{3.4}{5}=2,4\left(cm\right)\)
b
Áp dụng đl pytago vào tam giác AHC vuông tại H có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{60^2+144^2}=156\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A, đường cao AH có:
\(AC^2=HC.BC\Rightarrow BC=\dfrac{AC^2}{HC}=\dfrac{156^2}{144}=169\left(cm\right)\)
\(BH=BC-HC=169-144=25\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow AB=\sqrt{25.169}=65\left(cm\right)\)
c
Áp dụng đl pytago vào tam giác AHC vuông tại H:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{12^2-\left(\dfrac{60}{13}\right)^2}=\dfrac{144}{13}\approx11,08\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC đường cao AH có:
\(AH^2=HB.HC\Rightarrow HB=\dfrac{AH^2}{HC}=\dfrac{\left(\dfrac{60}{13}\right)^2}{\dfrac{144}{13}}=\dfrac{25}{13}\approx1,92\left(cm\right)\)
\(BC=HB+HC=\dfrac{25}{13}+\dfrac{144}{13}=13\left(cm\right)\)
\(AB^2=HB.BC\Rightarrow AB=\sqrt{HB.HC}=\sqrt{\dfrac{144}{13}.\dfrac{25}{13}}=\dfrac{60}{13}\approx4,62\left(cm\right)\)
Cho tam giác ABC vuông tại A, có đường cao AH (H thuộc BC). Biết độ dài đoạn AC bằng 5cm, đoạn HC bằng 4cm. Tính độ dài các cạnh AB và BC.
Xét \(\Delta AHC\left(\widehat{AHC}=90^o\right)\) có:
\(AC^2=AH^2+HC^2\) (định lí pitago)
\(\Rightarrow AH^2=AC^2-HC^2\)
\(\Rightarrow AH=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{AH^2}-\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}\)
\(\Rightarrow AB=3,75\left(cm\right)\)
Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC=\sqrt{3,75^2+5^2}=6,25\left(cm\right)\)
\(AH=\sqrt{AC^2-HC^2}=3\left(cm\right)\)
\(HB=\dfrac{AH^2}{HC}=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=4+2,25=6,25(cm)
\(AB=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
Cho tam giác ABC vuông ở A , AB=6cm; AC=8cm; BC=10cm có đường cao AH cắt cạnh BC tại H, đường phân giác BD của góc ABC cắt AC tại D.
a) Tính độ dài các đoạn thẳng AD và DC .
b) Tính AH=?
a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
1, Cho tam giác ABC vuông tại A,đường cao AH
a, Cho biêt AB=3cm,BC=5cm.Tính độ dài đoạn thẳng BH,CH,AH và AC
b,Cho biết AH=60cm,CH=144cm.Tính độ dài đoạn thẳng AB,AC,BC và BH
2, Cho tam giác ABC vuông tại A, đường cao AH
Cho biết \(\dfrac{AB}{AC}\)=\(\dfrac{5}{6}\) và BC=122cm.Tính độ dài các đoạn thẳng BH,CH
Bài 2:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{25}{36}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: HB+HC=BC
\(\Leftrightarrow HC\cdot\dfrac{61}{36}=122\)
\(\Leftrightarrow HC=72\left(cm\right)\)
hay HB=50(cm)
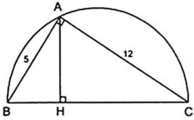
Cho tam giác ABC có AB = 5cm, AC = 12cm và BC = 13cm . Kẻ đường cao AH (H ∈ BC) . Tính độ dài các đoạn thẳng BH và CH.
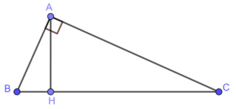
Ta có: A B 2 + A C 2 = 5 2 + 12 2 = 25 + 144 = 169 = 13 2 = B C 2
Suy ra, tam giác ABC vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: