a: \(A=0x^2y^4z+\dfrac{7}{2}x^2y^4z-\dfrac{2}{5}x^2y^4z=\dfrac{31}{10}x^2y^4z=\dfrac{31}{10}\cdot2^2\cdot\dfrac{1}{16}\cdot\left(-1\right)=-\dfrac{31}{40}\)

a: \(=\dfrac{7}{5}x^4z^3y=\dfrac{7}{5}\cdot2^4\cdot\left(-1\right)^3\cdot\dfrac{1}{2}=-\dfrac{56}{5}\)

b: \(=-xy^3\)

Bài 6:

M= 2.2 - 2.3+3.2.3

M= 4 - 6 + 18

M= 20

Bài 7: 

P= 1.2 - 5.-1.-2 + 8.-2.2

P = 2 -10 -32

P= -44

Bài 8:

A (thiếu dữ kiện bn ơi)

B= -1.2 . 3.2 + -1.3 +3.3 +-1.3

B= -2 . 6 + -3 + 9 +-3

B= -2 . 6 - 3 + 9 - 3

B= -12 - 3 + 9 - 3

B= -9

a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)

\(=\left(2x\right)^3-1^3-7x^3-7\)

\(=8x^3-1-7x^3-7=x^3-8\)

b: Thay x=-1/2 vào A, ta được:

\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)

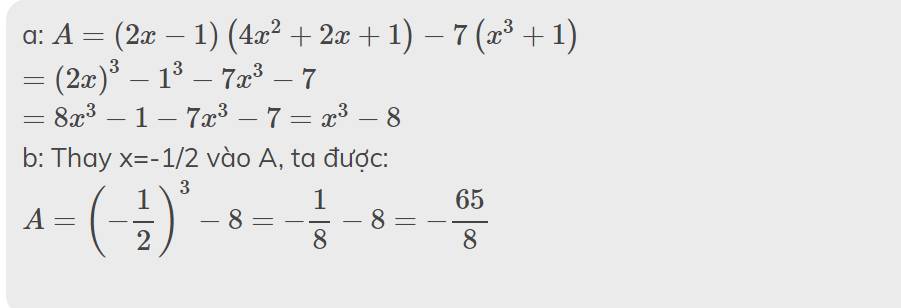
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)

Để A là số nguyên tố thì x-2=1

=>x=3

a. 2205 - (35 . 7)

= 2205 - 245

= 1960

b. 8700 : 25 . 4

= 348 . 4

= 1392

Bài 1: A = (\(\dfrac{7}{13}\) + \(\dfrac{6}{13}\)) x 100 - 13 x a

Thay a = 10 vào A ta có:

A = (\(\dfrac{7}{13}\) + \(\dfrac{6}{13}\)) x 100 -  13 x 10

A = \(\dfrac{13}{13}\) x 100 - 130

A = 100 - 130 

A = - 30

Thay a = 987 vào biểu thức A ta có:

A = (\(\dfrac{7}{13}\) + \(\dfrac{6}{13}\)) x 100 -  13 x 987

A = \(\dfrac{13}{13}\) x 100 - 12831

A =  100 - 12831

A = -12731

\(=3\times129+7\times71=387+497=884\)

ai giúp mình nhé

Bài 1 : 

\(N=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)

Ta có : \(x+y+z=0\Rightarrow x+y=-z;y+z=-x;x+z=-y\)

hay \(-z.\left(-x\right)\left(-y\right)=-zxy\)

mà \(xyz=2\Rightarrow-xyz=-2\)

hay N nhận giá trị -2 

Bài 2 : 

\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)Đặt \(a=10k;b=3k\)

hay \(\frac{30k-6k}{10k-9k}=\frac{24k}{k}=24\)

hay biểu thức trên nhận giá trị là 24 

c, Ta có : \(a-b=3\Rightarrow a=3+b\)

hay \(\frac{3+b-8}{b-5}-\frac{4\left(3+b\right)-b}{3\left(3+b\right)+3}=\frac{-5+b}{b-5}-\frac{12+4b-b}{9+3b+3}\)

\(=\frac{-5+b}{b-5}-\frac{12+3b}{6+3b}\)quy đồng lên rút gọn, đơn giản rồi 

1.Ta có:\(x+y+z=0\)

\(\Rightarrow\hept{\begin{cases}x+y=-z\\y+z=-x\\x+z=-y\end{cases}}\)

\(\Rightarrow N=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\left(-x\right)\left(-y\right)=-2\)

2.Ta có:\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)

Đặt \(\frac{a}{10}=\frac{b}{3}=k\Rightarrow a=10k;b=3k\)

Ta có:\(A=\frac{3a-2b}{a-3b}=\frac{3.10k-2.3k}{10k-3.3k}=\frac{30k-6k}{10k-9k}=\frac{k\left(30-6\right)}{k\left(10-9\right)}=24\)

Vậy....