Cho tam giác ABC vuông ở A có và AB = 6cm. Tính các cạnh của tam giác.

Những câu hỏi liên quan
1. cho tam giác abc vuông a có cạnh ab6cm, bc10cm.các đường phân giác trong và ngoài của góc b cắt ac lần lượt ở d và e. tính các đoạn thẳng bd và be2. cho tam giác abc vuông ở a, phân giác ad,đường cao ah. biết cd68cm, bd51cm. tính bh,hc3. cho tam giác abc có góc b60 độ, ac13cm và bc-ba7cm. tính độ dài các cạnh ab,bc4. cho tam giác abc cân ở b và điểm d trên cạnh ac. biết góc bdc60 độ, ad3dm, dc8dm. tính ab
Đọc tiếp
1. cho tam giác abc vuông a có cạnh ab=6cm, bc=10cm.các đường phân giác trong và ngoài của góc b cắt ac lần lượt ở d và e. tính các đoạn thẳng bd và be
2. cho tam giác abc vuông ở a, phân giác ad,đường cao ah. biết cd=68cm, bd=51cm. tính bh,hc
3. cho tam giác abc có góc b=60 độ, ac=13cm và bc-ba=7cm. tính độ dài các cạnh ab,bc
4. cho tam giác abc cân ở b và điểm d trên cạnh ac. biết góc bdc=60 độ, ad=3dm, dc=8dm. tính ab
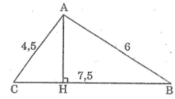
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. Chứng minh tam giác ABC vuông ở A. Tính các góc B , C và đường cao AH của tam giác
Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
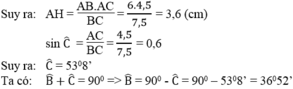
Đúng 0
Bình luận (0)
BÀI TẬP
Bài 1. Cho tam giác ABC có AB=5cm; AC=7cm. So sánh <B và <C
Bài 2. Cho tam giác ABC có AB=3cm; AC= 4cm;BC = 5cm. So sánh các góc của
tam giác
Bài 3.Cho tam giác có <B=60 0 ; <C =40 0 . So sánh các cạnh của tam giác ABC
Bài 4. Cho tam giác ABC vuông ở A có AB= 6cm; BC = 10 cm
1/ Tính AC
2/ So sánh các góc của tam giác ABC
Cho tam giác ABC vuông tại A có AB=6cm AC=8cm
a)tính độ dài cạnh và so sánh các góc của tam giác ABC
$o$
Ta có:AB2+AC2=BC2
62+82=BC2
36+64=BC2
100=BC2
=)BC=10
=)BC>AC>AB=)A>B>C(ĐFCM)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A ,cạnh BC=7,5;AB=6cm . Gọi AH là đường cao của tam giác ABC. Tính CH
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=\left(BC-CH\right)BC\)
\(\Rightarrow36=\left(7,5-CH\right)7,5=56,25-7,5CH\)
\(\Leftrightarrow CH=\dfrac{27}{10}\)cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A , AB=6cm; AC=8cm; BC=10cm có đường cao AH cắt cạnh BC tại H, đường phân giác BD của góc ABC cắt AC tại D.
a) Tính độ dài các đoạn thẳng AD và DC .
b) Tính AH=?
a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
Đúng 1
Bình luận (0)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
Đúng 0
Bình luận (0)
BAI 5: Cho biết ABC = MNP = RST. a) Nếu ABC vuông tại A thì các tam giác còn lại có vuông không? Vì sao? b) Cho biết thêm góc A = 90*, góc S = 60* . Tính các góc còn lại của ba tam giác. c) Biết AB = 7cm; NP = 5cm; RT = 6cm. Tính các cạnh còn lại của ba tam giác và tính tổng chu vi của ba tam giác.
Cho hình tam giác ABC là tam giác vuông ở A , cạnh AB bằng 30cm, cạnh AC bằng 40cm, cạnh BC bằng 50cm. Trên AB lấy điểm D, trên AC lấy điểm E, sao cho BDEC là hình thang có hiểu cao bằng 6cm.
a) Tính độ dài 3 đường cao của tam giác ABC ?
b) Tính diện tích hình tam giác ADE ?
Xem thêm câu trả lời
cho tam giác ABC vuông tại A có AB = 6cm ; BC = 10cm trên cạnh BC lấy điểm D sao cho BD = 6cm vẽ đường vuông góc với BC cắt cạnh AC tại M câu a tính AC câu b tính chu vi tam giác ABC câu c chứng minh BM là đường phân giác của tam giác ABC

























