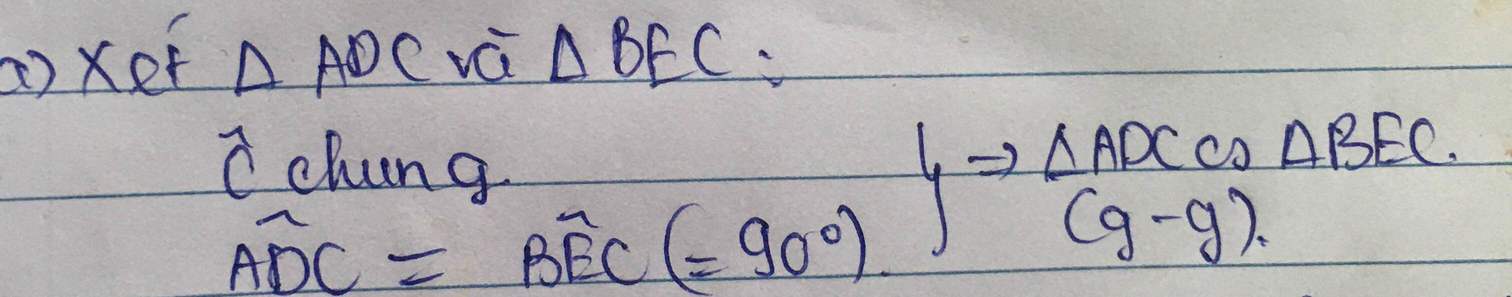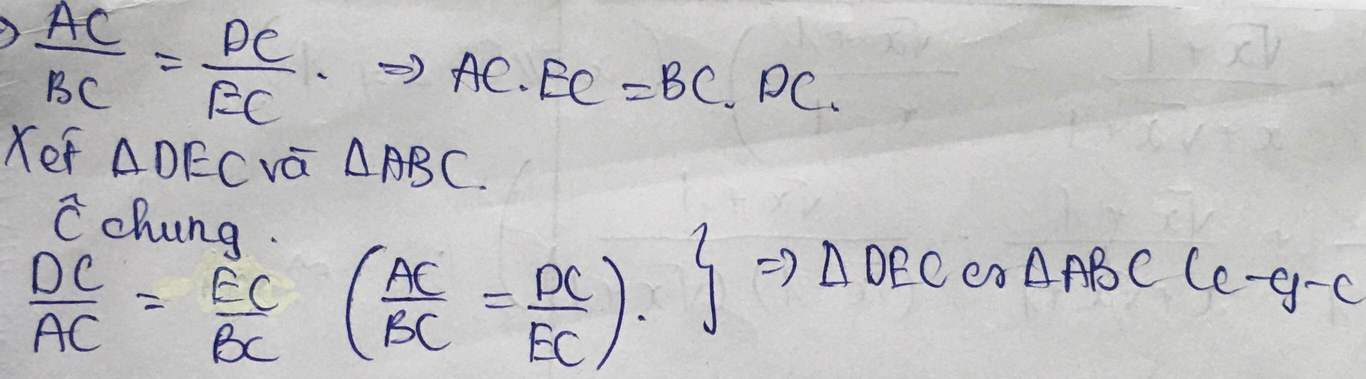cho tam giác ABC có 2 đường cao AD, BE
a) cm: adc đồng dạng bec
b) cm: ac.ec=bc.dc

Những câu hỏi liên quan
cho tam giác ABC có 2 đường cao AD, BE
a) cm: AC.EC=BC.DC
b) cm: tam giác DEC đồng dạng ABC
Cho tam giác ABC có hai đường cao là AD và BE ( D thuộc BC, E thuộc AC). Chứng minh rằng:
a) tam giác ADC đồng dạng tam giác BEC.
b) AC.EC=BC.DC
c) tam giác DEC đồng dạng tam giác ABC.
xét tam giác EBC và tam giác DAC có :
góc C chung
góc ADC = góc BEC = 90
=> tam giác EBC ~ tam giác DAC (g - g)
Đúng 0
Bình luận (0)
Cho tam giác ABC các đường cao AD và DE cắt nhau tại H CM
a, ADC đồng dạng BEC
b, AH.AD=AE.AC
c, AHB đồng dạng EHD
a: Xet ΔCEB vuông tại E và ΔCDA vuông tại D có
góc C chung
=>ΔCEB đồng dạng với ΔCDA
b: Xét ΔAEH vuông tại Evà ΔADC vuông tại D có
góc EAH chung
=>ΔAEH đồng dạng với ΔADC
=>AE/AD=AH/AC
=>AE*AC=AD*AH
c: Xét ΔHED và ΔHAB có
góc HED=góc HAB
góc EHD=góc AHB
=>ΔHED đồng dạng với ΔHAB
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a có ab = 12 cm ac = 16 cm. vẽ đường cao ah và đường phân giác AD của tam giác a) CM tam giác HBA đồng dạng với tâm giác ABC b) tìm tỉ số điện tích tam giác ABD và tam giác ADC c) tính BC, BD, AH d) tính điện tích tam giác AHD
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHAB đồng dạng với ΔACB
b: BD/CD=AB/AC=3/4
=>S ABD/S ACD=3/4
c: BC=căn 12^2+16^2=20cm
BD/3=CD/4=20/7
=>BD=60/7cm
AH=12*16/20=9,6cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AD là đường phân giác xuất phát từ đỉnh A . Gọi E và F lần lượt là hình chiếu của B và C trên AD .Chứng minh rằng :tam giác ABE đồng dạng vs tam giác ACF
Cm BH.BE+BC.DC = 4BM²Cm tanB.tanC =\(\frac{AD}{BD}\)1) cm : \(\Delta BHD\infty\Delta BCE\) \(\Rightarrow\frac{BH}{BC}=\frac{BD}{BE}\Rightarrow BH.BE=BC.BD\)
\(\Rightarrow BH.BE+BC.BD=BC.BD+BC.DC=BC^2\)
mà BC=2BM =>BC2=4BM2
=>\(\Rightarrow BH.BE+BC.DC=4BM^2\)
2) \(CM:\tan B=\frac{AD}{BD}\)
tan BHD =\(\frac{BD}{HD}\)
mà góc BHD= góc C
=>tan C=\(\frac{BD}{HD}\)
=> tanB.tanC=\(\frac{AD}{BD}.\frac{BD}{HD}=\frac{AD}{HD}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A=90°,đường cao AD,AB=8cm, AC=6cm.
a, CM tam giác BAC đồng dạng với tam giác ADC
b, Tính BC,AD
c, Kẻ DE vuông góc AB.CM tam giác AEH đồng dạng với tam giác ACB
Cho tam giác ABC có 3 đường cao AD,BE,CF cắt nhau tại H
a. CM : AH.HD=CH.HF
b. CM : tam giác CEH đồng dạng tam giác BEA
c. CM : FD.CH=CD.DH
d.cm: tam giác BDFđồng dạng tam gáic BAC
e.CM : FH là tia p/g của góc DEF
f. Gọi K là giao điểm của DF và BE. CM : HK.BE=BK.HE
cho tam giác abc vuông tại a có ab=3cm ac=5cm đường phân giác ad . đường vuông góc dc cắt ac ở ea, tam giác abc đồng dạng tam giác becb, tính bc, bd,ad
Xem chi tiết
a:
Sửa đề tam giác DEC
Xet ΔABC vuông tại A và ΔDEC vuông tại D có
góc C chung
=>ΔABC đồng dạng với ΔDEC
b: \(BC=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)
\(AD=\dfrac{2\cdot3\cdot5}{3+5}\cdot cos45=\dfrac{15\sqrt{2}}{8}\left(cm\right)\)
AD là phân giác
=>BD/AB=CD/AC
=>\(\dfrac{BD}{3}=\dfrac{CD}{5}=\dfrac{\sqrt{34}}{8}\)
=>\(BD=\dfrac{3\sqrt{34}}{8}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và có đường cao AD . Đường phận giác của góc ABC cắt AD ở F , cắt AC ở E .
a, CM tam giác ABC đồng dạng với tam giác ADC
b, Cm \(\frac{DF}{FA}=\frac{AE}{EC}\)
c, Cho AB = 3cm , AC = 4cm , BC = 5cm , Tính AE =?