Giải bài toán bài 3 bằng cách lập hệ phương trình

Những câu hỏi liên quan
cách giải các bài toán bằng cách lập phương trình hoặc hệ phương trình thường gặp ?
Bài 1 : Một Hcn có chu vi 600m. Nếu chiều dài giảm đi 1/5 của nó, chiều rộng tăng thêm 3/10 của nó thì chu vi Hcn không đổi. Tính chiều dài và chiều rộng của Hcn.
Giải bằng 2 cách :
Cách 1 : Giải bài toán bằng cách lập phương trình
Cách 2 ; Giải bài toán bằng cách lập hệ phương trình
Bài 1 : Một Hcn có chu vi 600m. Nếu chiều dài giảm đi 1/5 của nó, chiều rộng tăng thêm 3/10 của nó thì chu vi Hcn không đổi. Tính chiều dài và chiều rộng của Hcn.
Giải bằng 2 cách :
Cách 1 : Giải bài toán bằng cách lập phương trình
Cách 2 ; Giải bài toán bằng cách lập hệ phương trình
Cho hệ phương trình\(\hept{\begin{cases}x+y=40\\\left(x+3\right)\left(y+5\right)=xy+195\end{cases}}\)
Anh (chị) hãy thiết kế một bài toán thực tế mà khi giải bài toán bằng cách lập hệ
phương trình ta có hệ phương trình trên. Hãy giải bài toán đã thiết kế.
Ai thiết kế bài toán hộ cái. Bí chẳng có ý tưởng
Đề : Một hình chữ nhật có chu vi bằng 80 cm. Tăng chiều rộng lên 3cm; tăng chiều dài lên 5 cm thì diện tích tăng thêm 195 cm^2.
Tìm chiều dài và chiều rộng ban đầu.
Bài 1 : Số công nhân ở 2 xí nghiệp trước hia tỉ lệ với 2 và 3. Nay xí nghiệp I thêm 80 công nhân, xí nghiệp II thêm 40 công nhân, do đó số công nhân của 2 xí nghiệp tỉ lệ với 3 và 4. Tính số công nhân của 2 xí nghiệp hiện nay?
Giải bằng 2 cách :
Cách 1 : Giải bài toán bằng cách lập phương trình
Cách 2 : Giải bài toán bằng cách lập hệ phương trình
Bài 1 : Số công nhân ở 2 xí nghiệp trước hia tỉ lệ với 2 và 3. Nay xí nghiệp I thêm 80 công nhân, xí nghiệp II thêm 40 công nhân, do đó số công nhân của 2 xí nghiệp tỉ lệ với 3 và 4. Tính số công nhân của 2 xí nghiệp hiện nay?
Giải bằng 2 cách :
Cách 1 : Giải bài toán bằng cách lập phương trình
Cách 2 : Giải bài toán bằng cách lập hệ phương trình
Bài 1:Giải hệ phương trình bằng phương pháp cộng đại sốleft{{}begin{matrix}17x+4y213x+2y1end{matrix}right. Bài 2:Giải bài toán sau bằng cách lập hệ phương trìnhHai người đi xe máy cùng khởi hành một lúc từ 2 địa điểm A và B cách nhau 180km,đi ngược chiều nhau và gặp nhau sau 2 giờ.Tính vận tốc của hai người đó biết rằng vận tốc của người đi từ A bằng vận tốc người đi từ B
Đọc tiếp
Bài 1:Giải hệ phương trình bằng phương pháp cộng đại số
\(\left\{{}\begin{matrix}17x+4y=2\\13x+2y=1\end{matrix}\right.\)
Bài 2:Giải bài toán sau bằng cách lập hệ phương trình
Hai người đi xe máy cùng khởi hành một lúc từ 2 địa điểm A và B cách nhau 180km,đi ngược chiều nhau và gặp nhau sau 2 giờ.Tính vận tốc của hai người đó biết rằng vận tốc của người đi từ A bằng vận tốc người đi từ B
Bài 1:
Ta có: \(\left\{{}\begin{matrix}17x+4y=2\\13x+2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}17x+4y=2\\26x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-9x=0\\13x+2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(0;\dfrac{1}{2}\right)\)
Đúng 3
Bình luận (0)
Bài 2:
Gọi x(km/h) là vận tốc của người thứ nhất(Điều kiện: x>0)
Vận tốc của người thứ hai là: x(km/h)
Quãng đường người thứ nhất đi từ A đến chỗ gặp là: 2x(km)
Quãng đường người thứ hai đi từ B đến chỗ gặp là: 2x(km)
Theo đề, ta có: 2x+2x=180
\(\Leftrightarrow4x=180\)
hay x=45(thỏa ĐK)
Vậy: Vận tốc của hai người là 45km/h
Đúng 3
Bình luận (0)
Tìm 2 số tự nhiên biết 2 số đó hơn kém nhau 6a và tích chúng bằng 187
bài: giải bài toán bằng cách lập hệ phương trình
Giải bài toán bằng cách lập hệ phương trình:
Tổng của 2 số bằng 54. Ba lần số này hơn số kia là 2. Tìm hai số đó
Gọi 2 số cần tìm là x; y.
Tổng của 2 số là 59 nên ta có: x + y = 54
Ba lần số này hơn số kia là 2 nên: 3x – y =2
Ta có hệ phương trình:
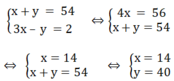
Vậy hai số cần tìm là 14 và 40.
Đúng 0
Bình luận (0)













