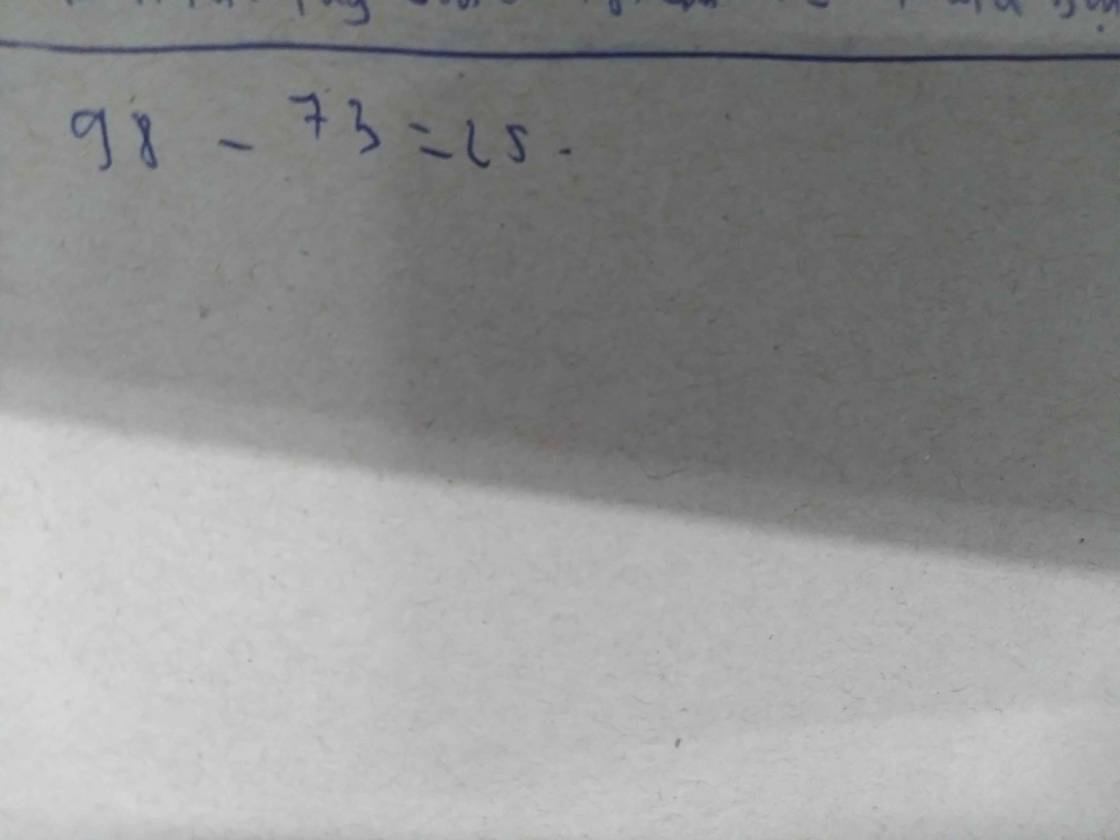112,7,20,4 sắp xếp thành phép chia và phép cộng
Những câu hỏi liên quan
18 ,16,160,8 sắp xếp thành phép nhân và phép cộng
dùng cả 10 chữ số từ 0 đến 9 sắp xếp cùng với phép cộng và phép nhân thành 1 biểu thức có giá trị là 2
0 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 + 2
dùng 2 phép toán cộng, trừ và các số từ 0 đến 9. Hãy sắp xếp thành một bài toán có kết quả là 100.
Cho các biểu thức đại số: 4xy2; 3 – 2y;
-
3
5
x2 y3x; 10x + y; 5(x + y); 2x2
-
1
2
y3x; 2x2y; -2y. Hãy sắp xếp chúng thành hai nhóm: Nhóm 1: Những biểu thức có chứa phép cộng, phép trừ. Nhóm 2: Các biểu thức còn lại.
Đọc tiếp
Cho các biểu thức đại số:
4xy2; 3 – 2y; - 3 5 x2 y3x; 10x + y;
5(x + y); 2x2 - 1 2 y3x; 2x2y; -2y.
Hãy sắp xếp chúng thành hai nhóm:
Nhóm 1: Những biểu thức có chứa phép cộng, phép trừ.
Nhóm 2: Các biểu thức còn lại.
Ta sắp xếp như sau:
Nhóm 1: 3 – 2y; 10x + y; 5(x+y)
Nhóm 2: 4xy2;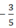 
x2 y3x; 2x2 
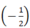y3x; 2x2y; -2y
Đúng 0
Bình luận (0)
trong 1 phép chia có dư , thương là 4 và số dư là 5. nếu cộng thêm 13 vào số bị chia , giữ nguyên số chia thì thương là 7 và số dư là 0(trở thành phép chia hết).Tìm số bị chia và số chia trong phép chia đầu tiên
Bài giải :
Sau khi cộng thêm 13 vào số bị chia thì thương tăng lên là :
7 - 4 = 3 ( lần )
Số chia trong phép chia là :
( 5 + 13 ) / 3 = 6
Số bị chia trong phép chia là :
6 * 4 + 5 = 29
Đáp số : số chia : 6
số bị chia : 26
Đúng 0
Bình luận (0)
xin lỗi bạn !
mk viết nhầm đáp số
số chia là 6 , còn số bị chia là 19 bn nhé !
Đúng 0
Bình luận (1)
số bị chia là 29 ms đúng bn nhé ! thành thật xin lỗi bn
Đúng 0
Bình luận (0)
Sắp xếp các đa thức sau rồi làm phép chia:
(24-x3+3x2+4x+9):(x2+1)
\(\dfrac{2x^4-x^3+3x^2+4x+9}{x^2+1}=\dfrac{2x^4+2x^2-x^3-x+x^2+1+5x+8}{x^2+1}\)
\(=2x^2-x+1+\dfrac{5x+8}{x^2+1}\)
Đúng 1
Bình luận (1)
SGK Kết nối tri thức với cuộc sống - Trang 65
17 tháng 3 2023 lúc 17:38
Anh Khoai phải sắp xếp các đốt tre thành phép tính đúng. Nhưng do vội quá nên anh xếp nhầm hai đốt tre. Em hãy xếp lại giúp anh Khoai nhé!
Phát biểu quy tắc chia hai đa thức một biến đã sắp xếp :
TH1: Quy tắc dành cho trường hợp phép chia hết.
TH2: Quy tắc dành cho trường hợp phép chia có dư.
cho hai đa thức P(x) 2x3 - 3x + x5 - 4x3 + 4x - x5 + x2 - 2Q(x) x3 - x2 + 3x + 1 + 3x2 và R(x) 3x2a) Thu gọn và sắp xếp đa thức theo luỹ thừa giảm dần của biến.c) Thực hiện phép chia P(x) cho Q(x)d) Thực hiện phép nhân P(x) cho R(x) và Q(x) cho R(x)
Đọc tiếp
cho hai đa thức P(x) = 2x3 - 3x + x5 - 4x3 + 4x - x5 + x2 - 2
Q(x) = x3 - x2 + 3x + 1 + 3x2 và R(x) = 3x2
a) Thu gọn và sắp xếp đa thức theo luỹ thừa giảm dần của biến.
c) Thực hiện phép chia P(x) cho Q(x)
d) Thực hiện phép nhân P(x) cho R(x) và Q(x) cho R(x)
Mình xp giúp được mỗi câu đầu thôi nha ;-;;;; 2 câu sau mình chưa học, bạn thông cảm ;-;;;.
`a,` \(\text{P(x) =}\)\(2x^3-3x+x^5-4x^3+4x-x^5+x^2-2\)
`P(x)= (2x^3 - 4x^3)-(3x-4x) +(x^5-x^5) +x^2-2`
`P(x)= -2x^3- (-x)+0+x^2-2`
`P(x)=-2x^3+x+x^2-2`
`Q(x)= x^3-x^2+3x+1+3x^2`
`Q(x)= x^3- (x^2-3x^2) +3x+1`
`Q(x)=x^3- (-2x^2)+3x+1`
Đúng 1
Bình luận (0)