Gọi ID là tia phân giác của góc MDN. Gọi góc EDK là góc đối đỉnh của IDM. Chứng minh rằng: EDK = ID

Những câu hỏi liên quan
Điền vào chỗ trống để chứng minh bài toán sau: Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM. Chứng minh rằngChừng minh:∠(IDM) ∠(IDN) (vì…) (1)∠(IDM) ∠(EDK) (vì…) (2)Từ (1) và (2) suy ra... Đó là điều phải chứng minh
Đọc tiếp
Điền vào chỗ trống để chứng minh bài toán sau: Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM. Chứng minh rằng
Chừng minh:
∠(IDM) =∠(IDN) (vì…) (1)
∠(IDM) =∠(EDK) (vì…) (2)
Từ (1) và (2) suy ra...
Đó là điều phải chứng minh

Chứng minh:
∠(IDM) =∠(IDN) (vì DI là tia phân giác của ∠(MDN) (1)
∠(IDM) =∠(EDK) (vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra ∠(EDK) =∠(IDN) (điều phải chứng minh)
Đúng 0
Bình luận (0)
Điền vào chỗ trống (.............) để chứng minh bài toán sau :
Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM.
Chứng minh rằng :
widehat{EDK}widehat{IDN}
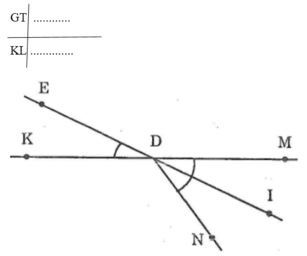
GT :
KL :
Chứng minh (h.10)
widehat{IDM}widehat{IDN} (vì ................) (1)
widehat{IDM}widehat{EDK} (vì ...............) (2)
Từ (1) và (2) suy ra ...............
Đó là điều phải chứng minh
Đọc tiếp
Điền vào chỗ trống (.............) để chứng minh bài toán sau :
Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM.
Chứng minh rằng :
\(\widehat{EDK}=\widehat{IDN}\)
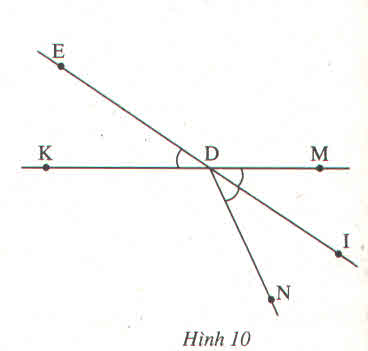
GT :
KL :
Chứng minh (h.10)
\(\widehat{IDM}=\widehat{IDN}\) (vì ................) (1)
\(\widehat{IDM}=\widehat{EDK}\) (vì ...............) (2)
Từ (1) và (2) suy ra ...............
Đó là điều phải chứng minh
GT: DI là tia phân giác của \(\widehat{MDN}\)
\(\widehat{EDK}\) đối đỉnh với \(\widehat{IDM}\)
KL: \(\widehat{EDK}=\widehat{IDM}\)
Chứng minh (h.10)
(vì DI là tia phân giác của \(\widehat{MDN}\)) (1)
(vì 2 góc này đối đỉnh) (2)
Từ (1) và (2) suy ra \(\widehat{EDK}=\widehat{IDN}\)
Đó là điều phải chứng minh.
Đúng 0
Bình luận (0)
GT:DI là tia phân giác của MDN^
EDK^ đối đỉnh với IDM^
KL:EDK^ = IDN^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Gọi DI là tia phân giác của góc MDN. Gọi góc EDK là góc đối đỉnh của góc IDM. Chứng minh góc EDK bằng góc IDN
Chứng minh:
\(\widehat{IDM}=\widehat{IDN}\) ( vì \(DI\) là tia pân giác của \(\widehat{MDN}\)) (1)
\(\widehat{IDM}=\widehat{EDK}\) ( hai góc đối đỉnh )
Từ (1) và (2) suy ra : \(\widehat{EDK}=\widehat{IDN}\left(đpcm\right)\)
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
Ta có: Chứng minh:IDM=IDN (Vì DI là tia phân giác của MDN ) (1)
Ta có: IDM=EDK (Vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra: EDK=IDN (điều phải chứng minh)
Đúng 0
Bình luận (0)
Bài 1: cho tam giác EKH có góc H= 60 độ. tia phân giác của góc K cắt EH tại D. tính góc EDK và KDH
Bài 2: cho tam giác ABC có góc B = góc C = 50 độ. gọi AM là tia phân giác của góc ngoài đỉnh A. CMR: AM // BC
1) đề thiếu nhé
2) Sửa lại : AM | BC
+) Góc A + B + C = 180o => A + 50o + 50o = 180o => A = 80o
=> góc BAM = A/2 = 40o
+) Tam giác BAM có: góc BAM + B + AMB = 180o => 40o + 50o + AMB = 180o => AMB = 90o
=> AM | BC
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn(AB<AC), vẽ hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh: Tam giác ABD đồng dạng với tam giác ACE
b)Chứng minh: góc ADE=góc ABC
c) Gọi K là giao điểm của AH và BC. CHứng minh : BD là tia phân giác của góc EDK
d) Chứng minh: BH.BD vuông góc CH.CE=BC.BC
Cho tam giác ABC có 3 góc nhọn, vẽ các đường cao BD,CE cắt nnhau tại H. gọi K là giao điểm của AH với BC.cm BD là tia phân giác của góc EDK
cho 2 góc AOB và COD là góc đối đỉnh. Gọi OM là tia phân giác của góc AOB và ON là tia phân giác của góc COD. Chứng minh tia OM là tia đối của tia ON.
vì hai góc AOB và COD là hai đối đỉnh mà hai góc đối đỉnh thì bằng nhau và 2goc đó mỗi góc được một tia phân giác phân thành hai góc bằng nhau và tạo thành một tia đối .
Đúng 0
Bình luận (0)
Cho xOy=50 độ, gọi xOt, yOv là 2 góc kề bù với xOy. Chứng minh rằng:
a) Hai góc xOt, yOv là 2 góc đối đỉnh. Tính số đo 2 góc đó.
b) Đường thẳng chứa tia phân giác của góc vOy cũng chứa tia phân giác tOx
cho 2 góc đối đỉnh : AOB và A'OB'. Gọi Ox là phân giác của AOB. Ox' là tia đối của Ox. Chứng tỏ rằng Ox là phân giác của góc AOB























